题目内容
在平面直角坐标系![]() 中,设点
中,设点![]() (1,0),直线
(1,0),直线![]() :
:![]() ,点
,点![]() 在直线
在直线![]() 上移动,
上移动,![]() 是线段
是线段![]() 与
与![]() 轴的交点,
轴的交点, ![]() .
.
(Ⅰ)求动点![]() 的轨迹的方程;
的轨迹的方程;
(Ⅱ) 记![]() 的轨迹的方程为
的轨迹的方程为![]() ,过点
,过点![]() 作两条互相垂直的曲线
作两条互相垂直的曲线![]() 的弦
的弦![]() 、
、![]() ,设
,设![]() 、
、![]() 的中点分别为
的中点分别为![]() .求证:直线
.求证:直线![]() 必过定点
必过定点![]() .
.

(Ⅰ)动点![]() 的轨迹
的轨迹![]() 是以
是以![]() 为焦点,
为焦点,![]() 为准线的抛物线,其方程为:
为准线的抛物线,其方程为:![]() .
.
(Ⅱ)见解析
解析:
(Ⅰ)依题意知,直线![]() 的方程为:
的方程为:![]() .点
.点![]() 是线段
是线段![]() 的中点,且
的中点,且![]() ⊥
⊥![]() ,∴
,∴![]() 是线段
是线段![]() 的垂直平分线.…………………….2分
的垂直平分线.…………………….2分
∴![]() 是点
是点![]() 到直线
到直线![]() 的距离.
的距离.
∵点![]() 在线段
在线段![]() 的垂直平分线,∴
的垂直平分线,∴![]() .…………4分
.…………4分
故动点![]() 的轨迹
的轨迹![]() 是以
是以![]() 为焦点,
为焦点,![]() 为准线的抛物线,其方程为:
为准线的抛物线,其方程为:![]() . ……….7分
. ……….7分
(Ⅱ) 设![]() ,
,![]() ,直线AB的方程为
,直线AB的方程为![]() …………….8分
…………….8分
则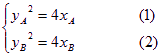
(1)—(2)得![]() ,即
,即![]() ,……………………………………9分
,……………………………………9分
代入方程![]() ,解得
,解得![]() .
.
所以点M的坐标为![]() .……………………………………10分
.……………………………………10分
同理可得:![]() 的坐标为
的坐标为![]() .
.
直线![]() 的斜率为
的斜率为![]() ,方程为
,方程为
![]() ,整理得
,整理得![]() ,………………12分
,………………12分
显然,不论![]() 为何值,
为何值,![]() 均满足方程,
均满足方程,
所以直线![]() 恒过定点
恒过定点![]()
![]() .………………14
.………………14

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目