题目内容
已知函数f(x)和g(x)的图象关于原点对称,且f(x)=x2+2x,(1)求函数g(x)的解析式;
(2)解不等式g(x)≥f(x)-|x-1|;
(3)若h(x)=g(x)-λf(x)+1在[-1,1]上是增函数,求实数λ的取值范围.
解析:此题考查综合应用函数的奇偶性和增减性解决解析式和最值问题.
解:(1)设函数y=f(x)的图象上任一点Q(x0,y0)关于原点的对称点为P(x,y),?
则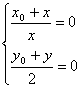 即
即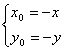
∵点Q(x0,y0)在函数y=f(x)的图象上,?
∴-y=x2-2x,即y=-x2+2x.?
故g(x)=-x2+2x.?
(2)由g(x)≥f(x)-|x-1|,可得2x2-|x-1|≤0.?
当x≥1时,2x2-x+1≤0.?
此时不等式无解.?
当x<1时,2x2-x+1≤0.?
∴-1≤x≤![]() .?
.?
因此,原不等式的解集为[-1, ![]() ].?
].?
(3)h(x)=-(1+λ)x2+2(1-λ)x+1.?
①当λ=-1时,h(x)=4x+1在[-1,1]上是增函数,∴λ=-1.?
②当λ≠-1时,对称轴的方程为x=![]() .
.
(ⅰ)当λ<-1时,![]() ≤-1,解得λ<-1.
≤-1,解得λ<-1.
(ⅱ)当λ>-1时,![]() ≥1时,解得-1<λ≤0.?
≥1时,解得-1<λ≤0.?
综上,λ≤0.

练习册系列答案
相关题目
已知函数f(x)和g(x)分别由下表给出定义:
| x | 1 | 2 | 3 |
| f(x) | 2 | ________ | 3 |
| x | 1 | 2 | 3 |
| g(x) | 3 | ________ | 1 |
若方程f(g(x))=g(f(x))的解恰有2个,请在表中横线上填上合适的数.
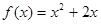
 ;
;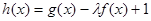 在[-1,1]上是增函数,求实数
在[-1,1]上是增函数,求实数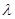 的取值范围。
的取值范围。