题目内容
选做题:(本小题共3小题,请从这3题中选做2小题,如果3题都做,则按所做的前两题记分,每小题7分.)(1)(矩阵与变换)在直角坐标系中,已知△ABC的顶点坐标为A(0,0)、B(1,1)、C(0,2),矩阵M=
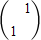 ,N=
,N=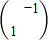 ,求△ABC在矩阵MN作用下变换所得的图形的面积;
,求△ABC在矩阵MN作用下变换所得的图形的面积;(2)(坐标系与参数方程)极坐标系下,求直线
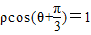 与圆
与圆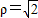 的公共点个数;
的公共点个数;(3)(不等式)已知x+2y=1,求x2+y2的最小值.
【答案】分析:(1)由矩阵的乘积可求MN然后可在△ABC内任意取一点(x,y)则根据变换的定义可得点(x,y)在MN矩阵的变换下得到点(x,-y)结合对称性可求.
(2)利用两角和的余弦公式可将直线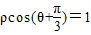 化为
化为 ρcosθ
ρcosθ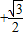 ρsinθ=1,再结合极坐标的定义x=ρcosθ,y=ρsinθ,ρ=
ρsinθ=1,再结合极坐标的定义x=ρcosθ,y=ρsinθ,ρ= 可得直线和圆的普通方程分别为x-
可得直线和圆的普通方程分别为x-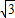 y-2=0,x2+y2=2而要考查直线和圆的公共点得个数只需判断圆心到直线的距离和半径的大小即可.
y-2=0,x2+y2=2而要考查直线和圆的公共点得个数只需判断圆心到直线的距离和半径的大小即可.
(3)结合题设和要求的结果联想到要利用柯西不等式(a2+b2)(c2+d2)≥(ac+bd)2当且仅当ac=bd时等号成立.
解答:解:(1)∵MN=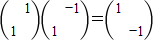
∴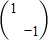
 =
=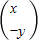
∴在矩阵MN的作用下,一个图形变换为与之关于x轴对称的图形,
因此△ABC在矩阵MN作用下变换所得到的图形与△ABC全等,从而其面积等于△ABC的面积,即为1.
(2)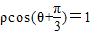 的普通方程为
的普通方程为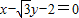 ,
,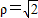 的普通方程为x2+y2=2
的普通方程为x2+y2=2
则圆心到直线的距离为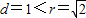 ,所以直线和圆相交,故有两个交点.
,所以直线和圆相交,故有两个交点.
(3)∵
∴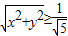
∴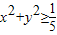 ,当且仅当:
,当且仅当: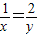 ,即y=2x时取等号,
,即y=2x时取等号,
∴x+4x=5x=1
∴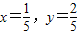 时,x2+y2的最小值为
时,x2+y2的最小值为 .
.
点评:第一题考查了矩阵的变换,关键是的分析出三角形在矩阵MN的变换下得出的是什么图形.第二题考查了极坐标的有关知识和直线和圆的位置关系的判定,解此题的关键是要会借助x=ρcosθ,y=ρsinθ,ρ=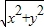 将直线和圆的极坐标方程化为普通方程然后利用圆心到直线的距离公式求出圆心到直线的距离再与圆的半径作大小比较即可得解.
将直线和圆的极坐标方程化为普通方程然后利用圆心到直线的距离公式求出圆心到直线的距离再与圆的半径作大小比较即可得解.
(2)利用两角和的余弦公式可将直线
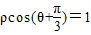 化为
化为 ρcosθ
ρcosθ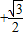 ρsinθ=1,再结合极坐标的定义x=ρcosθ,y=ρsinθ,ρ=
ρsinθ=1,再结合极坐标的定义x=ρcosθ,y=ρsinθ,ρ= 可得直线和圆的普通方程分别为x-
可得直线和圆的普通方程分别为x-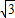 y-2=0,x2+y2=2而要考查直线和圆的公共点得个数只需判断圆心到直线的距离和半径的大小即可.
y-2=0,x2+y2=2而要考查直线和圆的公共点得个数只需判断圆心到直线的距离和半径的大小即可.(3)结合题设和要求的结果联想到要利用柯西不等式(a2+b2)(c2+d2)≥(ac+bd)2当且仅当ac=bd时等号成立.
解答:解:(1)∵MN=
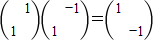
∴
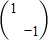
 =
=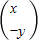
∴在矩阵MN的作用下,一个图形变换为与之关于x轴对称的图形,
因此△ABC在矩阵MN作用下变换所得到的图形与△ABC全等,从而其面积等于△ABC的面积,即为1.
(2)
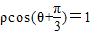 的普通方程为
的普通方程为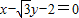 ,
,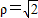 的普通方程为x2+y2=2
的普通方程为x2+y2=2则圆心到直线的距离为
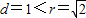 ,所以直线和圆相交,故有两个交点.
,所以直线和圆相交,故有两个交点.(3)∵

∴
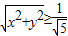
∴
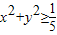 ,当且仅当:
,当且仅当: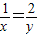 ,即y=2x时取等号,
,即y=2x时取等号,∴x+4x=5x=1
∴
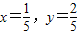 时,x2+y2的最小值为
时,x2+y2的最小值为 .
.点评:第一题考查了矩阵的变换,关键是的分析出三角形在矩阵MN的变换下得出的是什么图形.第二题考查了极坐标的有关知识和直线和圆的位置关系的判定,解此题的关键是要会借助x=ρcosθ,y=ρsinθ,ρ=
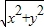 将直线和圆的极坐标方程化为普通方程然后利用圆心到直线的距离公式求出圆心到直线的距离再与圆的半径作大小比较即可得解.
将直线和圆的极坐标方程化为普通方程然后利用圆心到直线的距离公式求出圆心到直线的距离再与圆的半径作大小比较即可得解. 
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (t为参数)与直线4x+ky=1垂直,则常数k= .
(t为参数)与直线4x+ky=1垂直,则常数k= .