题目内容
(本大题共2个小题,任选一题作答,若做两题,则按所做的第(1)题给分,共5分)
(1)曲线ρ=2cosθ关于直线θ=
对称的曲线的极坐标方程为
(2)(不等式选讲)在区间[t,t+1]上满足不等式|x3-3x+1|≥1的解有且只有一个,则实数t的取值范围为
(1)曲线ρ=2cosθ关于直线θ=
| π |
| 4 |
ρ=2sinθ.
ρ=2sinθ.
(2)(不等式选讲)在区间[t,t+1]上满足不等式|x3-3x+1|≥1的解有且只有一个,则实数t的取值范围为
(0,
-1)
| 3 |
(0,
-1)
.| 3 |
分析:(1)先将原极坐标方程ρ=2cosθ两边同乘以ρ后化成直角坐标方程,再结合曲线关于直线的对称性,利用直角坐标方程解决问题.
(2)先在R上求解不等式|x3-3x+1|≥1,然后根据不等式的解集确定“在区间[t,t+1]上满足不等式|x3-3x+1|≥1的解有且只有一个”t的范围.
(2)先在R上求解不等式|x3-3x+1|≥1,然后根据不等式的解集确定“在区间[t,t+1]上满足不等式|x3-3x+1|≥1的解有且只有一个”t的范围.
解答:解:(1)解:将原极坐标方程ρ=2cosθ,化为:
ρ2=2ρcosθ,
化成直角坐标方程为:x2+y2-2x=0,
它关于直线y=x(即θ=
)对称的圆的方程是
x2+y2-2y=0,其极坐标方程为:ρ=2sinθ
故答案为:ρ=2sinθ.
(2)由不等式|x3-3x+1|≥1,得出x3-3x+1≥1①或x3-3x+1≤-1②,
解①得-
≤x≤0或x≥
解②得解②得x≤-2或x=1
∴不等式|x3-3x+1|≥1的解集为{x|x≤-2或-
≤x≤0或x≥
或x=1}
∵在区间[t,t+1]上满足不等式|x3-3x+1|≥1的解有且只有一个
∴0<t<
-1
故答案为:(0,
-1)
ρ2=2ρcosθ,
化成直角坐标方程为:x2+y2-2x=0,
它关于直线y=x(即θ=
| π |
| 4 |
x2+y2-2y=0,其极坐标方程为:ρ=2sinθ
故答案为:ρ=2sinθ.
(2)由不等式|x3-3x+1|≥1,得出x3-3x+1≥1①或x3-3x+1≤-1②,
解①得-
| 3 |
| 3 |
解②得解②得x≤-2或x=1
∴不等式|x3-3x+1|≥1的解集为{x|x≤-2或-
| 3 |
| 3 |
∵在区间[t,t+1]上满足不等式|x3-3x+1|≥1的解有且只有一个
∴0<t<
| 3 |
故答案为:(0,
| 3 |
点评:(1)本题考查点的极坐标和直角坐标的互化,利用直角坐标与极坐标间的关系:ρcosθ=x,ρsinθ=y,ρ2=x2+y2,进行代换即得
(2)本题考查绝对值不等式的解法,过程中应用了因式分解求解不等式,增加了题目的难度.
(2)本题考查绝对值不等式的解法,过程中应用了因式分解求解不等式,增加了题目的难度.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
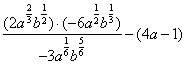
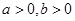 ,化简:
,化简: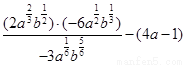
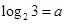 ,
,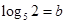 ,试用
,试用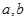 表示
表示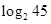
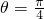 对称的曲线的极坐标方程为________
对称的曲线的极坐标方程为________