题目内容
选做题(本大题共2个小题.任选一题作答)
①若直线
(t为参数)与直线4x+ky=1垂直,则常数k=
②不等式|x+1|-|x-3|≥0的解集是_
①若直线
|
3
3
.②不等式|x+1|-|x-3|≥0的解集是_
(-∞,-2)
(-∞,-2)
.分析:①把直线的参数方程化为普通方程,根据两直线垂直,则他们的斜率之积等于-1,解方程求得k 的值.
②不等式 即|x+1|>|x-3|,平方可得 x2+2x+1>x2+6x+9,由此求得不等式的解集.
②不等式 即|x+1|>|x-3|,平方可得 x2+2x+1>x2+6x+9,由此求得不等式的解集.
解答:解:①直线
(t为参数)消去参数化为
=
,即 3x-4y-7=0,
根据它与直线4x+ky=1垂直,可得
×
=-1,解得 k=3,
故答案为 3.
②不等式|x+1|-|x-3|≥0 即|x+1|>|x-3|,平方可得 x2+2x+1>x2+6x+9,
解得 x<-2,
故答案为(-∞,-2).
|
| 1-x |
| 2 |
| y-2 |
| 3 |
根据它与直线4x+ky=1垂直,可得
| 3 |
| 4 |
| -4 |
| k |
故答案为 3.
②不等式|x+1|-|x-3|≥0 即|x+1|>|x-3|,平方可得 x2+2x+1>x2+6x+9,
解得 x<-2,
故答案为(-∞,-2).
点评:本题主要考查把参数方程化为普通方程的方法,两直线垂直的性质,绝对值不等式的解法,属于中档题.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目
 无实数解,则a的取值范围是
。
无实数解,则a的取值范围是
。 ,(α为参数)与曲线
,(α为参数)与曲线 的交点个数为 个。
的交点个数为 个。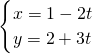 (t为参数)与直线4x+ky=1垂直,则常数k=________.
(t为参数)与直线4x+ky=1垂直,则常数k=________. (t为参数)与直线4x+ky=1垂直,则常数k= .
(t为参数)与直线4x+ky=1垂直,则常数k= . 无实数解,则a的取值
无实数解,则a的取值 范围是 。
范围是 。 ②(极坐标参数方程选做题)曲线
②(极坐标参数方程选做题)曲线 ,(α为参数)与曲线
,(α为参数)与曲线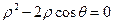 的交点个数为 个。
的交点个数为 个。