题目内容
下列命题:
①终边在坐标轴上的角的集合是{α|α=
,k∈Z};
②若2sinx=1+cosx,则tan
必为
;
③ab=0,asinx+bcosx=
sin(x+φ),(|φ|<π)中,若a>0,则φ=arctan
;
④函数y=sin(
x-
)在区间[-
,
]上的值域为[-
,
];
⑤方程sin(2x+
)-a=0在区间[0,
]上有两个不同的实数解x1,x2,则x1+x2=
.
其中正确命题的序号为______.
①终边在坐标轴上的角的集合是{α|α=
| kπ |
| 2 |
②若2sinx=1+cosx,则tan
| x |
| 2 |
| 1 |
| 2 |
③ab=0,asinx+bcosx=
| a2+b2 |
| b |
| a |
④函数y=sin(
| 1 |
| 2 |
| π |
| 6 |
| π |
| 3 |
| 11π |
| 6 |
| ||
| 2 |
| ||
| 2 |
⑤方程sin(2x+
| π |
| 3 |
| π |
| 2 |
| π |
| 6 |
其中正确命题的序号为______.
①由于终边在x轴上的角的集合为{α|α=kπ=
,k∈Z},终边在y轴上的角的集合为{α|α=kπ+
=
,k∈Z}所以终边在坐标轴上的角的集合为{α|α=kπ=
,k∈Z}∪{α|α=kπ+
=
,k∈Z}={α|α=
,k∈Z}故①对
②由于当x=π时2sinx=1+cosx仍成立但tan
=tan
没意义故②错
③当ab≠0时asinx+bcosx=
(
sinx+
cosx)由于(
)2+(
)2=1故可令cos∅=
则sin∅=
所以asinx+bcosx=
sin(x+φ)(|φ|<π)中,若a>0,则φ=arctan
故③对
④令t=
x-
则由于x∈[-
,
]故t∈[-
,
]结合函数y=sint在t∈[-
,
]上的图象可知其值域为[-
,1]故④错
⑤令y=sin(2x+
)=sint则t∈[
,
]在同一直角坐标系中作出y=sint,t∈[
,
]的图象和y=a使得两图象有两个交点则可得t1+t2=π即2x1+
+2x2+
=π所以x1+x2=
故⑤对
故答案为 ①③⑤
| 2kπ |
| 2 |
| π |
| 2 |
| (2k+1)π |
| 2 |
| 2kπ |
| 2 |
| π |
| 2 |
| (2k+1)π |
| 2 |
| kπ |
| 2 |
②由于当x=π时2sinx=1+cosx仍成立但tan
| x |
| 2 |
| π |
| 2 |
③当ab≠0时asinx+bcosx=
| a2+b2 |
| a | ||
|
| b | ||
|
| a | ||
|
| b | ||
|
| a | ||
|
| b | ||
|
| a2+b2 |
| b |
| a |
④令t=
| 1 |
| 2 |
| π |
| 6 |
| π |
| 3 |
| 11π |
| 6 |
| π |
| 3 |
| 3π |
| 4 |
| π |
| 3 |
| 3π |
| 4 |
| ||
| 2 |
⑤令y=sin(2x+
| π |
| 3 |
| π |
| 3 |
| 4π |
| 3 |
| π |
| 3 |
| 4π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| π |
| 6 |
故答案为 ①③⑤

练习册系列答案
 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
 、
、 都是单位向量,则
都是单位向量,则 ;
; ;
; 、
、 与
与 是三个非零向量,则
是三个非零向量,则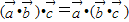 ;
; 与
与 共线,当且仅当有唯一一个实数λ,使得
共线,当且仅当有唯一一个实数λ,使得 成立.
成立.