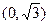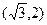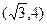题目内容
点(3,1)和(-4,6)在直线3x-2y+a=0的两侧,则a的范围是( )
A.a<7或a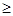 24 24 | B.-7<a<24 | C.a=-7或a=24 | D.以上都不对 |
B
分析:由已知点A(3,1)和B(-4, 6)分布在直线-3x+2y+a=0的两侧,我们将A,B两点坐标代入直线方程所得符号相反,则我们可以构造一个关于a的不等式,解不等式即可得到答案.
解答:解:若A(3,1)和B(-4,6)分布在直线-3x+2y+a=0的两侧
则[3×3-2×1+a]×[3×(-4)-2×6+a]<0
即(a+7)(a-24)<0
解得-7<a<24
故答案为:B
点评:本题考查的知识点是二元一次不等式与平面区域,根据A、B在直线两侧,则A、B坐标代入直线方程所得符号相反构造不等式是解答本题的关键.
解答:解:若A(3,1)和B(-4,6)分布在直线-3x+2y+a=0的两侧
则[3×3-2×1+a]×[3×(-4)-2×6+a]<0
即(a+7)(a-24)<0
解得-7<a<24
故答案为:B
点评:本题考查的知识点是二元一次不等式与平面区域,根据A、B在直线两侧,则A、B坐标代入直线方程所得符号相反构造不等式是解答本题的关键.

练习册系列答案
相关题目
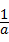 <
<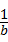 <0,则下列不等式①a+b<ab;②|a|>|b|;③a<b;④
<0,则下列不等式①a+b<ab;②|a|>|b|;③a<b;④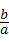 +
+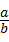 >2中,正确的不等式有( )
>2中,正确的不等式有( )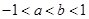 ,则
,则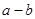 的范围是( )
的范围是( )



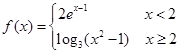 ,则不等式
,则不等式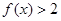 的解集为( )
的解集为( )
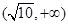
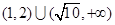
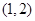
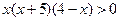 的解集是
的解集是  .
.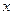 、
、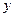 同时满足
同时满足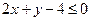 ,
,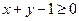 , 则目标函数
, 则目标函数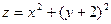 的最小值是 .
的最小值是 .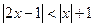
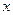 不等式
不等式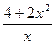
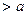 恒成
恒成 立,则实数
立,则实数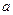 的取值范围是 ▲ .
的取值范围是 ▲ .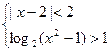 的解集为
的解集为