题目内容
已知复数z=
在复平面内对应的点在一、三象限的角平分线上,则
=( )
| 2a-i |
| i |
. |
| z |
| A、-1-i | ||||
| B、-1+i | ||||
C、-
| ||||
D、-
|
分析:利用复数的除法运算化简素数z,然后由实部等于虚部求解实数a的值,代入z后求得
.
. |
| z |
解答:解:由z=
=
=-1-2ai.
∵复数z=
在复平面内对应的点在一、三象限的角平分线上,
∴-1=-2a,
解得:a=
.
∴z=-1-i,
=-1+i.
故选:B.
| 2a-i |
| i |
| (2a-i)•(-i) |
| -i2 |
∵复数z=
| 2a-i |
| i |
∴-1=-2a,
解得:a=
| 1 |
| 2 |
∴z=-1-i,
. |
| z |
故选:B.
点评:本题考查了复数的代数表示法及其几何意义,考查了复数的除法运算,是基础的计算题.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
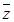 及|
及|