题目内容
已知指数函数y=g(x)满足:g(2)=4,定义域为R上的函数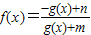 是奇函数.
是奇函数.(Ⅰ)求y=g(x)与y=f(x)的解析式;
(Ⅱ)判断y=f(x)在R上的单调性并用单调性定义证明;
(Ⅲ)若方程f(x)=b在(-∞,0)上有解,试证:-1<3f(b)<0.
【答案】分析:(I)根据指数函数y=g(x)满足:g(2)=4,即可求出y=g(x)的解析式;由题意知f(0)=0,f(1)=-f(-1),解方程组即可求出m,n的值,即可求出y=f(x)的解析式;
(Ⅱ)任取x1,x2∈R,且x1<x2,根据指数函数的图象和性质,判断f(x1)-f(x2)的符号,进而根据函数单调性的定义可判断y=f(x)在R上的单调性
(Ⅲ)若方程f(x)=b,可得b∈(0,1),进而可得f(1)<f(b)<f(0),进而得到结论.
解答:解:(I)设g(x)=ax(a>0,a≠1),由g(2)=4得a=2,故g(x)=2x,…(2分)
∵函数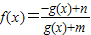 =
= 是奇函数
是奇函数
∴f(0)=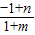 =0
=0
∴n=1;又由f(1)=-f(-1)知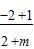 =-
=-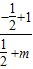 ,解得m=1
,解得m=1
∴f(x)=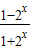
(II)f(x)=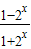 在(-∞,+∞)上为减函数,理由如下:
在(-∞,+∞)上为减函数,理由如下:
设x1,x2∈R,且x1<x2,
∴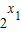 <
<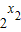 ,1+
,1+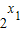 >0,1+
>0,1+ >0,
>0,
∴f(x1)-f(x2)= -
-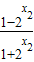 =
= >0
>0
即f(x1)>f(x2)
故f(x)=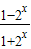 在(-∞,+∞)上为减函数
在(-∞,+∞)上为减函数
证明:(III)若方程f(x)=b在(-∞,0)上有解,
即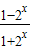 =
=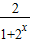 -1=b在(-∞,0)上有解,
-1=b在(-∞,0)上有解,
∵此时2x∈(0,1)
∴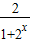 -1∈(0,1)
-1∈(0,1)
从而b∈(0,1)
由(II)得f(x)=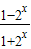 在(-∞,+∞)上为减函数
在(-∞,+∞)上为减函数
∴f(1)<f(b)<f(0).
即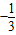 <f(b)<0
<f(b)<0
即:-1<3f(b)<0
点评:本题考查的知识点:待定系数法求指数函数的解析式,函数的奇偶性和函数单调性的性质,方程的根与函数零点的关系,是函数问题的简单综合应用,难度中档
(Ⅱ)任取x1,x2∈R,且x1<x2,根据指数函数的图象和性质,判断f(x1)-f(x2)的符号,进而根据函数单调性的定义可判断y=f(x)在R上的单调性
(Ⅲ)若方程f(x)=b,可得b∈(0,1),进而可得f(1)<f(b)<f(0),进而得到结论.
解答:解:(I)设g(x)=ax(a>0,a≠1),由g(2)=4得a=2,故g(x)=2x,…(2分)
∵函数
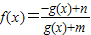 =
= 是奇函数
是奇函数∴f(0)=
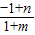 =0
=0∴n=1;又由f(1)=-f(-1)知
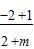 =-
=-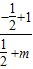 ,解得m=1
,解得m=1∴f(x)=
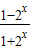
(II)f(x)=
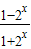 在(-∞,+∞)上为减函数,理由如下:
在(-∞,+∞)上为减函数,理由如下:设x1,x2∈R,且x1<x2,
∴
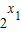 <
<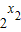 ,1+
,1+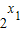 >0,1+
>0,1+ >0,
>0,∴f(x1)-f(x2)=
 -
-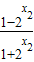 =
= >0
>0即f(x1)>f(x2)
故f(x)=
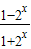 在(-∞,+∞)上为减函数
在(-∞,+∞)上为减函数证明:(III)若方程f(x)=b在(-∞,0)上有解,
即
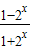 =
=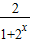 -1=b在(-∞,0)上有解,
-1=b在(-∞,0)上有解,∵此时2x∈(0,1)
∴
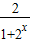 -1∈(0,1)
-1∈(0,1)从而b∈(0,1)
由(II)得f(x)=
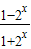 在(-∞,+∞)上为减函数
在(-∞,+∞)上为减函数∴f(1)<f(b)<f(0).
即
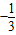 <f(b)<0
<f(b)<0即:-1<3f(b)<0
点评:本题考查的知识点:待定系数法求指数函数的解析式,函数的奇偶性和函数单调性的性质,方程的根与函数零点的关系,是函数问题的简单综合应用,难度中档

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目