题目内容
已知指数函数y=g(x)过点(1,3),函数f(x)=
是R上的奇函数.
(I)求y=g(x)的解析式;
(II)求n的值并用定义域判定y=f(x)的单调性;
(III)讨论关于x的方程xf(x)=m的解的个数.
| -g(x)+n | g(x)+1 |
(I)求y=g(x)的解析式;
(II)求n的值并用定义域判定y=f(x)的单调性;
(III)讨论关于x的方程xf(x)=m的解的个数.
分析:(I)根据指数函数y=g(x)满足:g(1)=3,即可求出y=g(x)的解析式;由题意知f(0)=0,解方程组即可求出n的值,即可求出y=f(x)的解析式;
(Ⅱ)任取x1,x2∈R,且x1<x2,根据指数函数的图象和性质,判断f(x1)-f(x2)的符号,进而根据函数单调性的定义可判断y=f(x)在R上的单调性;
(III)方程xf(x)=m即
=
,对字母m进行分类讨论,分别考察左右两边函数的图象的交点个数即可得出答案.
(Ⅱ)任取x1,x2∈R,且x1<x2,根据指数函数的图象和性质,判断f(x1)-f(x2)的符号,进而根据函数单调性的定义可判断y=f(x)在R上的单调性;
(III)方程xf(x)=m即
| -3x+1 |
| 3x+1 |
| m |
| x |
解答: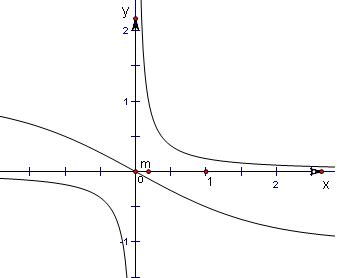 解:(I)设g(x)=ax(a>0,a≠1),由g(1)=3得a=3,故g(x)=3x,…(2分)
解:(I)设g(x)=ax(a>0,a≠1),由g(1)=3得a=3,故g(x)=3x,…(2分)
∵函数f(x)=
=
是奇函数
∴f(0)=
=0
∴n=1;
∴f(x)=
(II)f(x)=
在(-∞,+∞)上为减函数,理由如下:
设x1,x2∈R,且x1<x2,
∴f(x1)-f(x2)=
-
=
>0
即f(x1)>f(x2)
故f(x)在(-∞,+∞)上为减函数.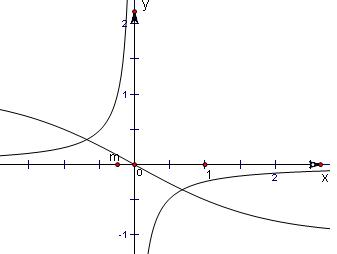
(III)方程xf(x)=m即
=
,
分别考察左右两边函数的图象,
当m>0时,两图象没有交点,即方程xf(x)=m的解的个数为0;
当m=0时,两图象有一个交点,即方程xf(x)=m的解的个数为1;
当m<0时,两图象有两个交点,即方程xf(x)=m的解的个数为2;
 解:(I)设g(x)=ax(a>0,a≠1),由g(1)=3得a=3,故g(x)=3x,…(2分)
解:(I)设g(x)=ax(a>0,a≠1),由g(1)=3得a=3,故g(x)=3x,…(2分)∵函数f(x)=
| -g(x)+n |
| g(x)+1 |
| -3x+n |
| 3x+1 |
∴f(0)=
| -30+n |
| 30+1 |
∴n=1;
∴f(x)=
| -3x+1 |
| 3x+1 |
(II)f(x)=
| -3x+1 |
| 3x+1 |
设x1,x2∈R,且x1<x2,
∴f(x1)-f(x2)=
| -3x1+1 |
| 3x1+1 |
| -3x2+1 |
| 3x2+1 |
| 2(2x2-2x1) |
| (1+2x1)(1+2x2) |
即f(x1)>f(x2)
故f(x)在(-∞,+∞)上为减函数.

(III)方程xf(x)=m即
| -3x+1 |
| 3x+1 |
| m |
| x |
分别考察左右两边函数的图象,
当m>0时,两图象没有交点,即方程xf(x)=m的解的个数为0;
当m=0时,两图象有一个交点,即方程xf(x)=m的解的个数为1;
当m<0时,两图象有两个交点,即方程xf(x)=m的解的个数为2;
点评:本题考查的知识点:待定系数法求指数函数的解析式,函数的奇偶性和函数单调性的性质,方程的根与函数零点的关系,是函数问题的简单综合应用,难度中等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目