题目内容
设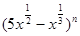 的展开式的各项系数之和是
的展开式的各项系数之和是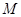 ,二项式系数之和是
,二项式系数之和是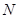 ,且
,且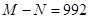 ,则
,则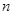 的值是( )
的值是( )
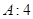
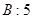
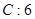
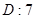
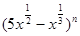 的展开式的各项系数之和是
的展开式的各项系数之和是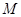 ,二项式系数之和是
,二项式系数之和是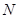 ,且
,且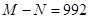 ,则
,则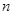 的值是( )
的值是( )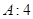
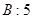
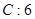
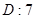
B
分析:利用赋值法求出展开式的各项系数和,据展开式的二项式系数和为2n,列出方程求出n;利用二项展开式的通项公式求出第r+1项,令x的指数为2求出展开式中x2项的系数.
解答:解:令x=1得M=4n,又N=2n,
∵M-N=992,∴4n-2n=992,
令2n=k,则k2-k-992=0,
∴k=32,∴n=5,
∵Tr+1=C5r(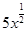 )5-r(-
)5-r(- )r
)r
=(-1)r?C5r?55-r?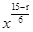 ,
,
令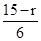 =2,得r=3,
=2,得r=3,
∴x2项系数为(-1)3C53?52=-250.
故选项为B
点评:本题考查利用赋值法求展开式的各项系数和;二项展开式的二项式系数的性质;利用二项展开式的通项公式求展开式的特定项.
解答:解:令x=1得M=4n,又N=2n,
∵M-N=992,∴4n-2n=992,
令2n=k,则k2-k-992=0,
∴k=32,∴n=5,
∵Tr+1=C5r(
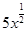 )5-r(-
)5-r(- )r
)r=(-1)r?C5r?55-r?
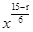 ,
,令
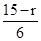 =2,得r=3,
=2,得r=3,∴x2项系数为(-1)3C53?52=-250.
故选项为B
点评:本题考查利用赋值法求展开式的各项系数和;二项展开式的二项式系数的性质;利用二项展开式的通项公式求展开式的特定项.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
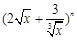 展开式中存在常数项,则n的值可以是 ( )
展开式中存在常数项,则n的值可以是 ( )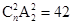 ,则
,则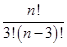 的值为 ( )
的值为 ( )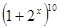 的展开式中的第
的展开式中的第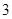 项为
项为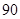 ,则
,则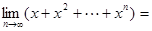 ___________.
___________.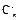 +2
+2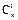 =11,∴m+2n=11,x2的系数为
=11,∴m+2n=11,x2的系数为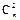 +22
+22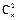 =
=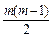 +2n(n-1)=
+2n(n-1)=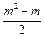 +(11-m)(
+(11-m)(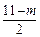 -1)=(m-
-1)=(m-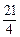 )2+
)2+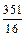 .
. 33,
33,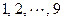 的
的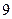 个小正方形(如下图),
个小正方形(如下图),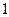 、
、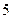 、
、
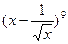 的展开式中的常数项为
的展开式中的常数项为