题目内容
（2008•深圳二模）在△ABC中，A=
，cosB=
．
（1）求cosC；
（2）设BC=
，求
•
的值．
| π |
| 4 |
| ||
| 10 |
（1）求cosC；
（2）设BC=
| 5 |
| CA |
| CB |
分析：（1）由C=π-（A+B），及A=
，cosB=
，故可用cosC=-cos(
+B)利用余弦和角公式求出余弦值；
（2）由正弦定理求出AC的值，由公式
•
=|
|•|
|•cosC求出内积的值
| π |
| 4 |
| ||
| 10 |
| π |
| 4 |
（2）由正弦定理求出AC的值，由公式
| CA |
| CB |
| CA |
| CB |
解答：解：（1）由cosB=
，B∈（0，π），得sinB=
…（2分）
∵C=π-（A+B），∴cosC=-cos(
+B)，…（4分）
∴cosC=-cos
cosB+sin
sinB
∴cosC=
…（7分）
（2）根据正弦定理得
=
，⇒AC=
，…（9分）
由sinB=
，得AC=
=
=3，…（12分）
∴
•
=|
|•|
|•cosC=3．…（14分）
| ||
| 10 |
3
| ||
| 10 |
∵C=π-（A+B），∴cosC=-cos(
| π |
| 4 |
∴cosC=-cos
| π |
| 4 |
| π |
| 4 |
∴cosC=
| ||
| 5 |
（2）根据正弦定理得
| BC |
| sinA |
| AC |
| sinB |
| BC•sinB |
| sinA |
由sinB=
3
| ||
| 10 |
| BC•sinB |
| sinA |
| ||||||
|
∴
| CA |
| CB |
| CA |
| CB |
点评：本题考查正弦定理及数量积公式、余弦的和角公式，解题的关键是熟练掌握定理与公式，利用定理公式建立方程求出未知量，本题是基本概念考查题，涉及到的公式较多，综合性强，易因为知识掌握不全导致解题失败，掌握全面基础知识是正确解此类题的保障．
练习册系列答案
阳光试卷单元测试卷系列答案
相关题目
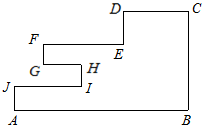（2008•深圳二模）一个质点从A出发依次沿图中线段到达B、C、D、E、F、G、H、I、J各点，最后又回到A（如图所示），其中：AB⊥BC，AB∥CD∥EF∥HG∥IJ，BC∥DE∥FG∥HI∥JA．欲知此质点所走路程，至少需要测量n条线段的长度，则n=（ ）
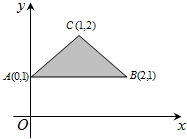（2008•深圳二模）当点M（x，y）在如图所示的三角形ABC内（含边界）运动时，目标函数z=kx+y取得最大值的一个最优解为（1，2），则实数k的取值范围是（ ）
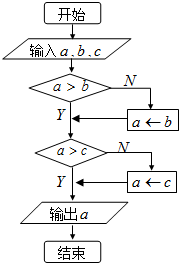（2008•深圳二模）如图所示的算法中，令a=tanθ，b=sinθ，c=cosθ，若在集合