题目内容
(2008•深圳二模)已知数列{an}满足a1=a,an+1=
(n∈N*).
(Ⅰ)试判断数列{
}是否为等比数列?若不是,请说明理由;若是,试求出通项an.
(Ⅱ)如果a=1时,数列{an}的前n项和为Sn.试求出Sn,并证明
+
+…+
<
(n≥3).
| (4n+6)an+4n+10 |
| 2n+1 |
(Ⅰ)试判断数列{
| an+2 |
| 2n+1 |
(Ⅱ)如果a=1时,数列{an}的前n项和为Sn.试求出Sn,并证明
| 1 |
| S3 |
| 1 |
| S4 |
| 1 |
| Sn |
| 1 |
| 10 |
分析:(Ⅰ)由an+1+2=
+2=
,知
=2•
.令bn=
,则bn+1=2bn.由此能够求出an=
•2n-1-2.
(Ⅱ)当a=1时,an=(2n+1)•2n-1-2,Sn=3+5•2+7•22+…+(2n+1)•2n-1-2n.令Tn=3+5•2+7•22+…+(2n+1)•2n-1,则2Tn=3•2+5•22+…+(2n-1)•2n-1+(2n+1)•2n,再由错位相减法和裂项求和法进行求解.
| (4n+6)an+4n+10 |
| 2n+1 |
| (4n+6)(an+2) |
| 2n+1 |
| an+1+2 |
| 2n+3 |
| (an+2) |
| 2n+1 |
| an+2 |
| 2n+1 |
| (a+2)(2n+1) |
| 3 |
(Ⅱ)当a=1时,an=(2n+1)•2n-1-2,Sn=3+5•2+7•22+…+(2n+1)•2n-1-2n.令Tn=3+5•2+7•22+…+(2n+1)•2n-1,则2Tn=3•2+5•22+…+(2n-1)•2n-1+(2n+1)•2n,再由错位相减法和裂项求和法进行求解.
解答:解:(Ⅰ)∵an+1+2=
+2=
,
∴
=2•
.
令bn=
,则bn+1=2bn. …2分
∵b1=
,
∴当a=-2时,b1=0,则bn=0.
∵数列{0}不是等比数列.
∴当a=-2时,数列{
}不是等比数列.…4分
当a≠-2时,b1≠0,则数列{
}是等比数列,且公比为2.
∴bn=b1•2n-1,
即
=
•2n-1.
解得an=
•2n-1-2. …6分
(Ⅱ)由(Ⅰ)知,当a=1时,an=(2n+1)•2n-1-2,
Sn=3+5•2+7•22+…+(2n+1)•2n-1-2n.
令Tn=3+5•2+7•22+…+(2n+1)•2n-1,…①
则2Tn=3•2+5•22+…+(2n-1)•2n-1+(2n+1)•2n,…②
由①-②:-Tn=3+2(2+22+…+2n-1)-(2n+1)•2n
=3+2•
-(2n+1)•2n
=(1-2n)•2n-1,
∴Tn=(2n-1)•2n+1,…9分
则Sn=Tn-2n=(2n-1)(2n-1). …10分
∵2n=Cn0+Cn1+…+Cnn-1+Cnn,
∴当n≥3时,2n≥Cn0+Cn1+Cnn-1+Cnn=2(n+1),则2n-1≥2n+1.…12分
∴Sn≥(2n-1)(2n+1),
则
≤
=
(
-
).…13分
因此,
+
+…+
≤
[(
-
)+(
-
)+…+(
-
)]=
(
-
)<
. …14分.
| (4n+6)an+4n+10 |
| 2n+1 |
| (4n+6)(an+2) |
| 2n+1 |
∴
| an+1+2 |
| 2n+3 |
| (an+2) |
| 2n+1 |
令bn=
| an+2 |
| 2n+1 |
∵b1=
| a+2 |
| 3 |
∴当a=-2时,b1=0,则bn=0.
∵数列{0}不是等比数列.
∴当a=-2时,数列{
| an+2 |
| 2n+1 |
当a≠-2时,b1≠0,则数列{
| an+2 |
| 2n+1 |
∴bn=b1•2n-1,
即
| an+2 |
| 2n+1 |
| a+2 |
| 3 |
解得an=
| (a+2)(2n+1) |
| 3 |
(Ⅱ)由(Ⅰ)知,当a=1时,an=(2n+1)•2n-1-2,
Sn=3+5•2+7•22+…+(2n+1)•2n-1-2n.
令Tn=3+5•2+7•22+…+(2n+1)•2n-1,…①
则2Tn=3•2+5•22+…+(2n-1)•2n-1+(2n+1)•2n,…②
由①-②:-Tn=3+2(2+22+…+2n-1)-(2n+1)•2n
=3+2•
| 2(1-2n-1) |
| 1-2 |
=(1-2n)•2n-1,
∴Tn=(2n-1)•2n+1,…9分
则Sn=Tn-2n=(2n-1)(2n-1). …10分
∵2n=Cn0+Cn1+…+Cnn-1+Cnn,
∴当n≥3时,2n≥Cn0+Cn1+Cnn-1+Cnn=2(n+1),则2n-1≥2n+1.…12分
∴Sn≥(2n-1)(2n+1),
则
| 1 |
| Sn |
| 1 |
| (2n-1)(2n+1) |
| 1 |
| 2 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
因此,
| 1 |
| S3 |
| 1 |
| S4 |
| 1 |
| Sn |
| 1 |
| 2 |
| 1 |
| 5 |
| 1 |
| 7 |
| 1 |
| 7 |
| 1 |
| 9 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
| 1 |
| 2 |
| 1 |
| 5 |
| 1 |
| 2n+1 |
| 1 |
| 10 |
点评:本题考查数列与不等式的综合运用,解题时要认真审题,注意错位相减法和裂项求和法的灵活运用.

练习册系列答案
相关题目
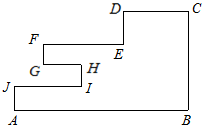 (2008•深圳二模)一个质点从A出发依次沿图中线段到达B、C、D、E、F、G、H、I、J各点,最后又回到A(如图所示),其中:AB⊥BC,AB∥CD∥EF∥HG∥IJ,BC∥DE∥FG∥HI∥JA.欲知此质点所走路程,至少需要测量n条线段的长度,则n=( )
(2008•深圳二模)一个质点从A出发依次沿图中线段到达B、C、D、E、F、G、H、I、J各点,最后又回到A(如图所示),其中:AB⊥BC,AB∥CD∥EF∥HG∥IJ,BC∥DE∥FG∥HI∥JA.欲知此质点所走路程,至少需要测量n条线段的长度,则n=( )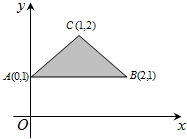 (2008•深圳二模)当点M(x,y)在如图所示的三角形ABC内(含边界)运动时,目标函数z=kx+y取得最大值的一个最优解为(1,2),则实数k的取值范围是( )
(2008•深圳二模)当点M(x,y)在如图所示的三角形ABC内(含边界)运动时,目标函数z=kx+y取得最大值的一个最优解为(1,2),则实数k的取值范围是( )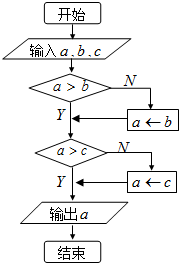 (2008•深圳二模)如图所示的算法中,令a=tanθ,b=sinθ,c=cosθ,若在集合
(2008•深圳二模)如图所示的算法中,令a=tanθ,b=sinθ,c=cosθ,若在集合