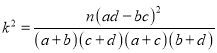题目内容
【题目】在党中央的英明领导下,在全国人民的坚定支持下,中国的抗击“新型冠状肺炎”战役取得了阶段性胜利,现在摆在我们大家面前的是有序且安全的复工复产.某商场为了提振顾客的消费信心,对某中型商品实行分期付款方式销售,根据以往资料统计,顾客购买该商品选择分期付款的期数ξ的分布列为

其中0<a<1,0<b<1.
(1)求购买该商品的3位顾客中,恰有1位选择分4期付款的概率;
(2)商场销售一件该商品,若顾客选择分4期付款,则商场获得的利润为2000元;若顾客选择分5期付款,则商场获得的利润为2500元;若顾客选择分6期付款,则商场获得的利润为3000元,假设该商场销售两件该商品所获得的利润为X(单位:元),
(i)设X=5500时的概率为m,求当m取最大值时,利润X的分布列和数学期望;
(ii)设某数列{xn}满足x1=0.4,xn=a,2xn+1=b,若a<0.25,求n的最小值.
【答案】(1)0.432(2)(i)详见解析(ii)2
【解析】
(1)方法1:设恰有一位顾客选择分4期付款的概率为P.由题可知:a+b=0.6,然后求解即可.
方法2:由于3位顾客中恰有1位选择“分4期付款”,则另外两位均不选“分4期付款”,利用相互独立事件乘法乘积求解概率即可.
(2)(ⅰ)由题可得X的值分别为4000,4500,5000,5500,6000.求出概率,得到分布列,然后求解期望即可.
(ⅱ)由题可得xn+2xn+1=a+b=0.6,得到![]() ,判断数列{xn﹣0.2}是等比数列,然后分类求解n的最小值.
,判断数列{xn﹣0.2}是等比数列,然后分类求解n的最小值.
(1)方法1:设恰有一位顾客选择分4期付款的概率为P.
由题可知:a+b=0.6,
则P=3×0.4×(a2+2ab+b2)=0.4×(a+b)2=0.4×0.62=0.432.
方法2:由于3位顾客中恰有1位选择“分4期付款”,则另外两位均不选“分4期付款”,所以P=3×0.4×(1﹣0.4)×(1﹣0.4)=0.432.
(2)(ⅰ)由题可得X的值分别为4000,4500,5000,5500,6000.
P(X=4000)=0.4×0.4=0.16,P(X=4500)=2×0.4×a=0.8a,
P(X=5000)=a2+2×0.4×b=a2+0.8b,
P(X=5500)=2ab,P(X=6000)=b2,
所以![]() ,
,
取最大值的条件为a=b=0.3
所以分布列为:
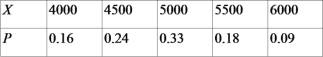
∴E(X)=4000×0.16+4500×0.24+5000×0.33+5500×0.18+6000×0.09=4900.
(ⅱ)解:由题可得xn+2xn+1=a+b=0.6,所以![]() ,
,
化简得![]() ,即{xn﹣0.2}是等比数列,首项为x1﹣0.2=0.2,公比为
,即{xn﹣0.2}是等比数列,首项为x1﹣0.2=0.2,公比为![]() ,
,
所以![]() ,化简得
,化简得![]()
由题可知:
①由题可知:![]() ,显然对所有n∈N*都成立;
,显然对所有n∈N*都成立;
②![]() ,也是对所有n∈N*都成立;
,也是对所有n∈N*都成立;
③![]() .
.
当n为偶数时,上述不等式恒成立;
当n为奇数时,![]() ,解得n>3.即n≥5
,解得n>3.即n≥5
综上所述,n的最小值为2.

【题目】2014年非洲爆发了埃博拉病毒疫情,在疫情结束后,当地防疫部门做了一项回访调查,得到如下结果,
患病 | 不患病 | |
有良好卫生习惯 | 20 | 180 |
无良好卫生习惯 | 80 | 220 |
(1)结合上面列联表,是否有![]() 的把握认为是否患病与卫生习惯有关?
的把握认为是否患病与卫生习惯有关?
(2)现从有良好卫生习惯且不患病的180人中抽取![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 共5人,再从这5人中选两人给市民做健康专题报告,求
共5人,再从这5人中选两人给市民做健康专题报告,求![]() ,
,![]() 至少有一人被选中的概率.
至少有一人被选中的概率.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |