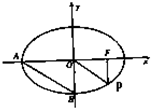
题目内容
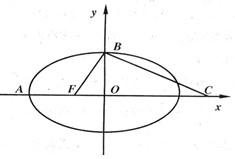 如图,F是椭圆
如图,F是椭圆| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
(Ⅰ)求椭圆的方程;
(Ⅱ)过点A的直线l与圆M交于P、Q两点,且
| MP |
| MQ |
分析:(Ⅰ)由题意知c=1,a=2,b=
,由此可知所求的椭圆方程为
+
=1.
(II)点A的坐标为(-2,0),圆M的方程为(x-1)2+y2=4,过点A斜率不存在的直线与圆不相交,设直线l2的方程为y=k(x+2.由此入手可知所求直线的方程为x+2
y+2=0或X-2
y+2=0.
| 3 |
| x2 |
| 4 |
| y2 |
| 3 |
(II)点A的坐标为(-2,0),圆M的方程为(x-1)2+y2=4,过点A斜率不存在的直线与圆不相交,设直线l2的方程为y=k(x+2.由此入手可知所求直线的方程为x+2
| 2 |
| 2 |
解答:解:(Ⅰ)F(-c,0),
∵椭圆的离心率为
,
∴∠FBO=300,∴b=
c,
∴B(0,
c),C(3c,0)
∴FC=4c=4,解得c=1,a=2,b=
∴所求的椭圆方程为
+
=1;(6分)
(II)点A的坐标为(-2,0),
圆M的方程为(x-1)2+y2=4,
过点A斜率不存在的直线与圆不相交,
设直线l2的方程为y=k(x+2),(7分)
∵
•
=-2,又|
|=|
|=2,
∴cos<MP,MQ>=
=-
. (9分)
∴∠PMQ=120°,圆心M到直线l2的距离d=
r=1,
所以
=1,
∴k=±
;
所求直线的方程为x+2
y+2=0或X-2
y+2=0. (12分)
∵椭圆的离心率为
| 1 |
| 2 |
∴∠FBO=300,∴b=
| 3 |
∴B(0,
| 3 |
∴FC=4c=4,解得c=1,a=2,b=
| 3 |
∴所求的椭圆方程为
| x2 |
| 4 |
| y2 |
| 3 |
(II)点A的坐标为(-2,0),
圆M的方程为(x-1)2+y2=4,
过点A斜率不存在的直线与圆不相交,
设直线l2的方程为y=k(x+2),(7分)
∵
| MP |
| MQ |
| MP |
| MQ |
∴cos<MP,MQ>=
| ||||
|
|
| 1 |
| 2 |
∴∠PMQ=120°,圆心M到直线l2的距离d=
| 1 |
| 2 |
所以
| |k+2k| | ||
|
∴k=±
| ||
| 4 |
所求直线的方程为x+2
| 2 |
| 2 |
点评:本题考查直线和椭圆的位置关系,解题时要认真审题,仔细解答.

练习册系列答案
相关题目
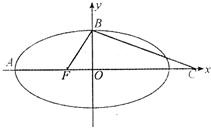 如图,F是椭圆
如图,F是椭圆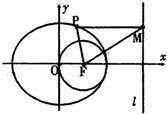 如图,F是椭圆的右焦点,以F为圆心的圆过原点O和椭圆的右顶点,设P是椭圆的动点,P到两焦点距离之和等于4
如图,F是椭圆的右焦点,以F为圆心的圆过原点O和椭圆的右顶点,设P是椭圆的动点,P到两焦点距离之和等于4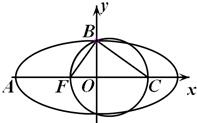 如图,F是椭圆
如图,F是椭圆