题目内容
如图是函数y=f（x）的导函数y=f′（x）的图象，下列说法正确的是①1是函数y=f（x）的极值点；
②-2是函数y=f（x）的极小值点
③y=f（x）在x=0处切线的斜率大于零；
④y=f（x）在区间（-2，2）上单调递增．
分析：由导函数的图象得到原函数的增减区间，然后逐一分析四个命题即可得到答案．
解答：解：由函数f（x）的导函数图象可知，
当x∈（-∞，-2）时，f′（x）＜0，原函数为减函数；
当x∈（-2，+∞）时，f′（x）≥0，原函数为增函数．
∴-2是函数y=f（x）的极小值点，故②正确；
∵f′（2）＞0，∴y=f（x）在x=0处切线的斜率大于零，故③正确；
当x∈（-2，+∞）时，f（x）为增函数，∴y=f（x）在区间（-2，2）上单调递增，故④正确；
∵x=1两侧导函数均大于0，∴1不是函数y=f（x）的极值点，故①不正确．
故答案为：（2）（3）（4）．
当x∈（-∞，-2）时，f′（x）＜0，原函数为减函数；
当x∈（-2，+∞）时，f′（x）≥0，原函数为增函数．
∴-2是函数y=f（x）的极小值点，故②正确；
∵f′（2）＞0，∴y=f（x）在x=0处切线的斜率大于零，故③正确；
当x∈（-2，+∞）时，f（x）为增函数，∴y=f（x）在区间（-2，2）上单调递增，故④正确；
∵x=1两侧导函数均大于0，∴1不是函数y=f（x）的极值点，故①不正确．
故答案为：（2）（3）（4）．
点评：本题考查了函数的单调性与导数之间的关系，需要注意的是极值点的导数等于0，但导数为0的点不一定是极值点，是基础题．
练习册系列答案
相关题目
4、如图是函数y=f（x）的图象，则下列说法正确的是（ ）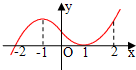
如图是函数y=f（x）的导函数y=f′（x）的图象，给出下列命题：
如图是函数y=f（x）的导函数y=f′（x）的图象，下列说法错误的是（ ）
（2012•茂名一模）如图是函数y=f（x）的导函数y=f′（x）的图象，给出下列命题：