题目内容
已知函数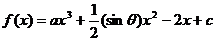 的图象过点
的图象过点 ,且在
,且在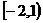 内单调递减,在
内单调递减,在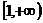 上单调递增.
上单调递增.
(1)求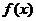 的解析式;
的解析式;
(2)若对于任意的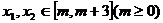 ,不等式
,不等式 恒成立,试问这样的
恒成立,试问这样的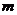 是否存在.若存在,请求出
是否存在.若存在,请求出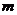 的范围,若不存在,说明理由
的范围,若不存在,说明理由
蚌埠二中2010---2012学年度高三十月质量检测数学(文)
【答案】
解: (1)∵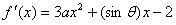 ,
,
由题设可知: 即
即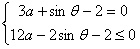
 sinθ≥1 ∴sinθ=1.
sinθ≥1 ∴sinθ=1.
从而a= 3,∴f(x)= 3x3+2xx+c,而又由f(1)= 6得c=3.
∴f(x)= 3x3+2xx+3即为所求.
(2)由 =(x+2)(x-1),易知f(x)在(-∞,-2)及(1,+∞)上均为增函数,在(-2,1)上为减函数.
=(x+2)(x-1),易知f(x)在(-∞,-2)及(1,+∞)上均为增函数,在(-2,1)上为减函数.
①当m>1时,f(x)在[m,m+3]上递增,故f(x)max=f(m+3), f(x)min=f(m)
由f(m+3)-f(m)= 3(m+3)3+2(m+3) (m+3)-3m3-2m2+2m=3m2+12m+2≤2,
得-5≤m≤1.这与条件矛盾,故 不存在.
② 当0≤m≤1时,f(x)在[m,1]上递增, 在[1,m+3]上递增
∴f(x)min=f(1), f(x)max=max{ f(m),f(m+3) },
又f(m+3)-f(m)= 3m2+12m+2=3(m+2)2-2>0(0≤m≤1)∴f(x)max= f(m+3)∴|f(x1)-f(x2)|≤f(x)max-f(x)min= f(m+3)-f(1)≤f(4)-f(1)= 2恒成立.
故当0≤m≤1时,原不等式恒成立.综上,存在m且m∈[0,1]合题意.

练习册系列答案
相关题目
 的图象过点A(3,7),则此函的最小值是 .
的图象过点A(3,7),则此函的最小值是 . 的图象过点
的图象过点 ,且图象上与点P最近的一个最低点是
,且图象上与点P最近的一个最低点是 .
. 的解析式;
的解析式; ,且
,且 为第三象限的角,求
为第三象限的角,求 的值;
的值; 在区间
在区间 上有零点,求
上有零点,求 的取值范围.
的取值范围. 的图象过点P(0,2),且在点M(-1,f(-1))处的切线方程为
的图象过点P(0,2),且在点M(-1,f(-1))处的切线方程为 .
. 的解析式; (2)求函数
的解析式; (2)求函数