题目内容
(2013•丽水一模)设向量
=(cosωx-sinωx,-1),
=(2sinωx,-1),其中ω>0,x∈R,已知函数f(x)=
•
的最小正周期为4π.
(Ⅰ)求ω的值;
(Ⅱ)若sinx0是关于t的方程2t2-t-1=0的根,且x0∈(-
,
),求f(x0)的值.
| a |
| b |
| a |
| b |
(Ⅰ)求ω的值;
(Ⅱ)若sinx0是关于t的方程2t2-t-1=0的根,且x0∈(-
| π |
| 2 |
| π |
| 2 |
分析:(Ⅰ)利用三角函数的恒等变换以及两个向量的数量积公式化简函数f(x)的解析式为
sin(2ωx+
),再根据周期求得ω的值.
(Ⅱ)求得 方程2t2-t-1=0的两根,可得sinx0=-
,可得x0的值,从而求得f(x0)的值.
| 2 |
| π |
| 4 |
(Ⅱ)求得 方程2t2-t-1=0的两根,可得sinx0=-
| 1 |
| 2 |
解答:解:(Ⅰ) f(x)=
•
=(cosωx-sinωx,-1)•(2sinωx,-1)=2sinωxcosωx-2sin2ωx+1
=sin2ωx+cos2ωx=
sin(2ωx+
),
因为 T=4π,所以,ω=
=4πω=
.…(6分)
(Ⅱ) 方程2t2-t-1=0的两根为 t1=-
,t2=1,
因为 x0∈(-
,
),所以 sinx0∈(-1,1),所以sinx0=-
,即x0=-
.
又由已知 f(x0)=
sin(
x0+
),
所以 f(-
)=
sin(-
+
)=
sin
=
.…(14分)
| a |
| b |
=sin2ωx+cos2ωx=
| 2 |
| π |
| 4 |
因为 T=4π,所以,ω=
| 2π |
| 2ω |
| 1 |
| 4 |
(Ⅱ) 方程2t2-t-1=0的两根为 t1=-
| 1 |
| 2 |
因为 x0∈(-
| π |
| 2 |
| π |
| 2 |
| 1 |
| 2 |
| π |
| 6 |
又由已知 f(x0)=
| 2 |
| 1 |
| 2 |
| π |
| 4 |
所以 f(-
| π |
| 6 |
| 2 |
| π |
| 12 |
| π |
| 4 |
| 2 |
| π |
| 6 |
| ||
| 2 |
点评:本题主要考查三角函数的恒等变换及化简求值,三角函数的周期性和求法,两个向量的数量积公式的应用,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
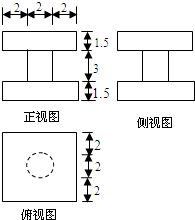 (2013•丽水一模)某几何体的三视图如图所示,则该几何体的体积为
(2013•丽水一模)某几何体的三视图如图所示,则该几何体的体积为 (2013•丽水一模)已知抛物线的顶点在坐标原点,焦点在y轴上,且过点(2,1),
(2013•丽水一模)已知抛物线的顶点在坐标原点,焦点在y轴上,且过点(2,1),