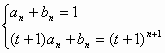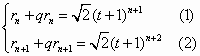Question

(1) 已知二次函数y＝f(x)在处取得最小值 (2) 若任意实数x都满足f(x)·g(x)＋anx＋bn＝xn+1(g(x)为多项式，n∈N+)，试用t表示an和bn (3) 设圆Cn的方程(x－an)2＋(y－bn)2＝rn2，圆Cn与Cn+1外切(n＝1，2，3，…)，{rn}是各项都是正数的等比数列，记Sn为前n个圆的面积之和，求rn，Sn．

Answer 1

答案：
解析：

(1)	设 ∴ 从而a＝1，∴
(2)	∴ 将x＝1，x＝t＋1分别代入上式，得 ∴，
(3)	∵an＋bn＝1，∴圆Cn的圆心On在直线x＋y＝1上， ∴ 又圆Cn与Cn+1外切，故rn＋rn+1，设{rn}的公比为q，则 (2)÷(1)，得于是 ∴