题目内容
(本小题满分12分)
为了加快经济的发展,某市选择A、B两区作为龙头带动周边地区的发展,决定在A、B两区的周边修建城际快速通道,假设A、B两区相距 个单位距离,城际快速通道所在的曲线为E,使快速通道E上的点到两区的距离之和为4个单位距离.
个单位距离,城际快速通道所在的曲线为E,使快速通道E上的点到两区的距离之和为4个单位距离.

(Ⅰ)以线段AB的中点O为原点建立如图所示的直角坐标系,求城际快速通道所在曲线E的方程;
(Ⅱ)若有一条斜率为 的笔直公路l与曲线E交于P,Q两点,同时在曲线E上建一个加油站M(横坐标为负值)满足
的笔直公路l与曲线E交于P,Q两点,同时在曲线E上建一个加油站M(横坐标为负值)满足 ,求
,求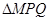 面积的最大值.
面积的最大值.
(Ⅰ) 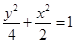 ;(Ⅱ)
;(Ⅱ) 面积的最大值为
面积的最大值为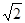 .
.
【解析】本试题主要是考查了圆锥曲线的 定义法求解轨迹方程,然后结合直线与椭圆的位置关系和点到线的距离和三角形的面积公式得到求解。
(1)因为设点T为曲线E上的任意一点,则|TA|+|TB|=4,|AB|=2,结合椭圆的定义得到曲线方程。
(2)设出直线PQ的方程与椭圆方程联立,得到关于x的一元二次方程,然后结合韦达定理和点到直线的距离公式表示出三角形的面积得到结论。
解:(Ⅰ)设点 为曲线
为曲线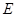 上的任意一点,则
上的任意一点,则
所以曲线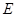 的轨迹为椭圆,
的轨迹为椭圆,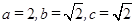 ,所以椭圆方程为
,所以椭圆方程为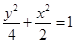 ………4分
………4分
(Ⅱ)设直线PQ的方程为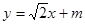 ,设
,设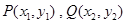
代入椭圆方程并化简得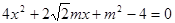 ,
,
由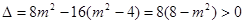 ,可得
,可得 . (
. ( ) …………………5分
) …………………5分
由 ,
,
故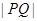
 .
………………………………7分
.
………………………………7分
又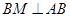 ,且
,且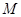 的横坐标又为负值,所以点
的横坐标又为负值,所以点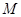 的坐标为
的坐标为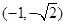
所以点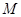 到
到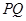 的距离为
的距离为 , ……………………………9分
, ……………………………9分
故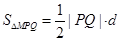
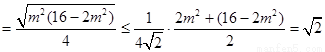 ,
,
当且仅当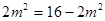 ,即
,即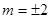 时取等号(满足
时取等号(满足 式)
式)
所以 面积的最大值为
面积的最大值为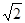 .
…………………………………12分
.
…………………………………12分

 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案