题目内容
设函数f(x)="|2x-1|+|2x-3|" , x∈R.
(Ⅰ)解不等式f(x)≤5;
(Ⅱ)若 的定义域为R,求实数m的取值范围.
的定义域为R,求实数m的取值范围.
(Ⅰ) {x∣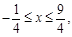 }. (Ⅱ) m >-2 。
}. (Ⅱ) m >-2 。
解析试题分析:(Ⅰ)∵ f(x)="|2x-1|+|2x-3|" , f(x)≤5
∴有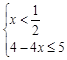 或
或 或
或
解得: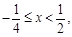 或
或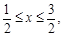 或
或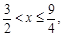
∴不等式的解集为:{x∣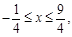 }. 5分
}. 5分
(Ⅱ) 若 的定义域为R,则f(x)+m≠0恒成立,
的定义域为R,则f(x)+m≠0恒成立,
即f(x)+m=0在R上无解.
又f(x)=|2x-1|+|2x-3|≥|2x-1-2x+3|=2,
∴f(x)最小值为2,
∴m >-2 10分
考点:本题主要考查绝对值不等式的解法,绝对值不等式恒成立问题。
点评:中档题,绝对值不等式的解法,应立足于“去绝对值符号”,一种思路是利用定义分类讨论,一种思路是通过平方,另一种思路是不去绝对值符号,利用几何意义。

练习册系列答案
相关题目
 是幂函数且在
是幂函数且在 上为减函数,函数
上为减函数,函数 在区间
在区间 上的最大值为2,试求实数
上的最大值为2,试求实数 的值。
的值。 在点
在点  处的切线
处的切线  平行直线
平行直线 ,且点
,且点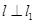 , 且
, 且  也过切点
也过切点 ,
,
 的单调区间;
的单调区间; ,且
,且 ,有
,有 ,求实数
,求实数 的取值范围.
的取值范围. 在
在 与
与 时都取得极值
时都取得极值 的值与函数
的值与函数 的单调区间
的单调区间 ,不等式
,不等式 恒成立,求
恒成立,求 的取值范围。
的取值范围。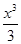 -x2-2ax(a∈R).
-x2-2ax(a∈R). 时,方程f(1-x)=
时,方程f(1-x)=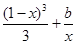 有实根,求实数b的最大值.
有实根,求实数b的最大值.