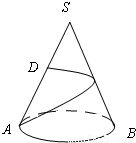
题目内容
如图，圆锥SAB的底面半径为R，母线长SA=3R，D为SA的中点，一个动点自底面圆周上的A点沿圆锥侧面移动到D，求这点移动的最短距离．分析：圆锥侧面展开成一个扇形，则对应的弧长是底圆周长2πR，沿圆锥侧面移动到D，利用余弦定理可求最短距离．
解答：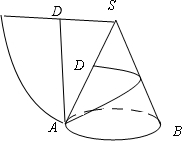
解：如图，圆锥侧面展开成一个扇形，则对应的弧长是底圆周长2πR，沿圆锥侧面移动到D，则最短距离为AD，
设∠ASD=α，则2πR=|α|×3R，∴|α|=
∴AD=
=
R
解：如图，圆锥侧面展开成一个扇形，则对应的弧长是底圆周长2πR，沿圆锥侧面移动到D，则最短距离为AD，设∠ASD=α，则2πR=|α|×3R，∴|α|=
| 2π |
| 3 |
∴AD=
9R2+
|
3
| ||
| 2 |
点评：本题考查余弦定理的运用，考查圆锥的侧面展开图，考查学生的计算能力，属于中档题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图所示，圆锥的轴截面为等腰直角△SAB，Q为底面圆周上一点．
（2009•杨浦区一模）如图，过圆锥轴的截面为等腰直角三角形SAB，Q为底面圆周上一点，已知
)，问能否确定θ，使得三棱锥C—SOD的体积最大？若能，求出体积的最大值和对应的θ；若不能，请说明理由．