Question

【题目】目前用外卖网点餐的人越来越多.现对大众等餐所需时间情况进行随机调查，并将所得数据绘制成频率分布直方图（如图）.其中等餐所需时间的范围是，样本数据分组为， ，，，．

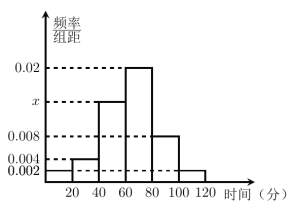
（1）求直方图中的值；

（2）某同学在某外卖网点了一份披萨，试估计他等餐时间不多于小时的概率；

（3）现有名学生都分别通过外卖网进行了点餐，这名学生中等餐所需时间少于小时的人数记为，求的分布列和数学期望．（以直方图中的频率作为概率）

Answer 1

【答案】（1）；（2）；（3）分布列见解析，数学期望

【解析】

（1）利用直方图概率的和为1，直接求解即可；
（2）根据直方图直接计算等餐时间不多于小时的概率；

（3）的可能取值为0，1，2，3，求出概率，得到分布列，然后求解期望.

解：（1）

解得；

（2）由直方图可得等餐时间不多于小时的概率，

所以他等餐时间不多于小时的概率为；

（3）这名学生中等餐所需时间少于小时的人数可取0,1,2,3

由（2）可知每个人等餐时间不超过1小时的概率为

所以 ，

，

那么的分布列为：

这名学生中等餐所需时间少于小时的人数的数学期望

.