题目内容
在直角坐标系中,曲线C1的参数方程为
|
| b |
| sinθ-cosθ |
分析:先消去参数θ得到曲线的普通方程,再利用直角坐标与极坐标间的关系,即利用ρcosθ=x,ρsinθ=y,ρ2=x2+y2,进行代换即得曲线C2在的直角坐标方程.在直角坐标系中画出它们的图形,由图观察即可得实数b的取值范围.
解答: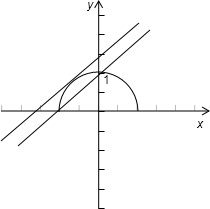 解:参数方程为
解:参数方程为
(t为参数),化成直角坐标方程为:
x2+y2=1,图象是圆心在原点半径为1的上半圆.
曲线C2在的直角坐标方程方程是:
x-y+b=0.
由圆心到直线的距离得:d=
=1,得到b=±
,
结合图象得:实数b的取值范围是1≤b<
.
故答案为:1≤b<
.
 解:参数方程为
解:参数方程为
|
x2+y2=1,图象是圆心在原点半径为1的上半圆.
曲线C2在的直角坐标方程方程是:
x-y+b=0.
由圆心到直线的距离得:d=
| |b| | ||
|
| 2 |
结合图象得:实数b的取值范围是1≤b<
| 2 |
故答案为:1≤b<
| 2 |
点评:本题考查点的极坐标和直角坐标的互化,圆的参数方程,体会数形结合的思想,能进行极坐标和直角坐标的互化.

练习册系列答案
相关题目