题目内容
（2013•天河区三模）（坐标系与参数方程选做题）
在直角坐标系中，曲线C1的参数方程为
（α为参数）；在极坐标系（以原点O为极点，以x轴正半轴为极轴）中，曲线C2的方程为ρ cos(θ+
)=
，则C1与C2两交点的距离为
在直角坐标系中，曲线C1的参数方程为
|
| π |
| 4 |
| 2 |
2
| 7 |
2
．| 7 |
分析：根据同角三角函数关系消去参数θ，即可求出曲线C1的普通方程，曲线C2的极坐标方程，根据极坐标公式进行化简就可求出直角坐标方程，利用直角坐标方程的形式，先求出圆心（0，0）到直线的距离，最后结合点到直线的距离公式弦AB的长度．
解答：解：由
得x2+y2=9，
∴曲线C1的普通方程为得x2+y2=9，
∵ρ（cosθ-sinθ）+2=0，
∴x-y+2=0，
曲线C2的方程为ρ cos(θ+
)=
，
∴曲线C2的直角坐标方程为x-y-2=0．
∵圆C1的圆心为（0，0），
∵圆心（0，0）到直线x-y-2=0的距离d=
=
，
又r=2，所以弦长AB=2
=2
．
则C1与C2两交点的距离为 2
．
故答案为：2
．
|
∴曲线C1的普通方程为得x2+y2=9，
∵ρ（cosθ-sinθ）+2=0，
∴x-y+2=0，
曲线C2的方程为ρ cos(θ+
| π |
| 4 |
| 2 |
∴曲线C2的直角坐标方程为x-y-2=0．
∵圆C1的圆心为（0，0），
∵圆心（0，0）到直线x-y-2=0的距离d=
| 2 | ||
|
| 2 |
又r=2，所以弦长AB=2
32-(
|
| 7 |
则C1与C2两交点的距离为 2
| 7 |
故答案为：2
| 7 |
点评：本题主要考查了圆的参数方程，以及简单曲线的极坐标方程，以及利用圆的几何性质计算圆心到直线的距等基本方法，属于基础题．
练习册系列答案
相关题目
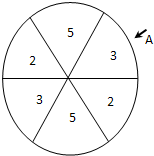（2013•天河区三模）如图，一个圆形游戏转盘被分成6个均匀的扇形区域．用力旋转转盘，转盘停止转动时，箭头A所指区域的数字就是每次游戏所得的分数（箭头指向两个区域的边界时重新转动），且箭头A指向每个区域的可能性都是相等的．在一次家庭抽奖的活动中，要求每个家庭派一位儿童和一位成人先后分别转动一次游戏转盘，得分情况记为（a，b）（假设儿童和成人的得分互不影响，且每个家庭只能参加一次活动）．