题目内容
【题目】已知函数![]() .
.
(1)若![]() ,求
,求![]() 的单调区间;
的单调区间;
(2)若![]() ,
,![]() ,求证:
,求证:![]() .
.
【答案】(1) ![]() 的单调递增区间为
的单调递增区间为![]() ,不存在递减区间.(2)见证明
,不存在递减区间.(2)见证明
【解析】
(1)求出![]() ,
,![]() 研究函数
研究函数![]() 的正负情况即可明确
的正负情况即可明确![]() 的正负情况,即可得到
的正负情况,即可得到![]() 的单调区间;
的单调区间;
(2) 设![]() ,证明
,证明![]() ,要证明
,要证明![]()
只需证明![]() .
.
解法一:(1)![]() 的定义域为
的定义域为![]() ,
,![]() 时,
时,![]()
![]() ,
,
所以![]()
当![]() 时,
时,![]() ,所以
,所以![]() 在
在![]() 单调递减;
单调递减;
当![]() 时,
时,![]() ,所以
,所以![]() 在
在![]() 单调递增;
单调递增;
所以![]() ,所以
,所以![]() 在
在![]() 单调递增,
单调递增,
即![]() 的单调递增区间为
的单调递增区间为![]() ,不存在递减区间.
,不存在递减区间.
(2)设![]() ,则
,则![]()
当![]() 时,
时,![]() ,所以
,所以![]() 在
在![]() 单调递增;
单调递增;
当![]() 时,
时,![]() ,所以
,所以![]() 在
在![]() 单调递减;
单调递减;
所以![]()
所以![]() 时,
时,![]()
即![]() ,要证明
,要证明![]()
只需证明![]()
由(1)知,![]() 在
在![]() 单调递增,
单调递增,
所以,当![]() 时,
时,![]() ,即
,即![]()
所以当![]() 时,
时,![]()
所以只需证明![]() ,即证明
,即证明![]()
设![]() ,则
,则![]()
所以![]() 在
在![]() 单调递增,所以
单调递增,所以![]() ,所以原不等式成立.
,所以原不等式成立.
综上,当![]() ,
,![]() 时,
时,![]()
解法二:(1)同解法一
(2)同解法一得只需证明![]()
设![]() ,则
,则![]()
![]() ,
,
由![]() 得
得![]() ,即
,即![]()
因为![]() ,所以
,所以![]()
又因为![]() ,所以
,所以![]()
因为![]() ,所以
,所以![]()
所以![]() ,
,![]() 在
在![]() 单调递增,所以
单调递增,所以![]()
所以![]() 在
在![]() 单调递减,所以
单调递减,所以![]() ,即
,即![]()
综上,当![]() ,
,![]() 时,
时,![]()
解法三:(1)同解法一
(2)同解法一得要证明![]() ,只需证明
,只需证明![]() ,
,
即证明![]() ,设
,设![]()
则![]()
由![]() ,得
,得![]() ,即
,即![]() ,所以
,所以![]() ,
,
所以![]() 在
在![]() 单调递增,所以
单调递增,所以![]()
即![]() ,所以
,所以![]()
综上,当![]() ,
,![]() 时,
时,![]()
解法四:(1)同解法一
(2)同解法一得要证明![]() ,只需证明
,只需证明![]() ,
,
即证明![]() ,设
,设![]()
![]() ,设
,设![]() ,
,
因为![]() ,所以
,所以![]() ,所以
,所以![]() 在
在![]() 单调递减,
单调递减,
所以![]() ,
,
所以![]() 在
在![]() 单调递增,所以
单调递增,所以![]()
即![]() ,所以
,所以![]()
综上,当![]() ,
,![]() 时,
时,![]()

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】现对某市工薪阶层关于“楼市限购令”的态度进行调查,随机抽调了50人,他们月收入的频数分布及对“楼市限购令”赞成人数如下表.
月收入(单位百元) |
|
|
|
|
|
|
频数 | 5 | 10 | 15 | 10 | 5 | 5 |
赞成人数 | 4 | 8 | 12 | 5 | 2 | 1 |
(1)由以上统计数据填下面2×2列联表,并问是否有99%的把握认为“月收入以5500元为分界点对“楼市限购令”的态度有差异;
月收入不低于55百元的人数 | 月收入低于55百元的人数 | 合计 | |
赞成 | a=______________ | c=______________ | ______________ |
不赞成 | b=______________ | d=______________ | ______________ |
合计 | ______________ | ______________ | ______________ |
(2)试求从年收入位于![]() (单位:百元)的区间段的被调查者中随机抽取2人,恰有1位是赞成者的概率。
(单位:百元)的区间段的被调查者中随机抽取2人,恰有1位是赞成者的概率。
参考公式: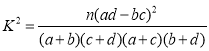 ,其中
,其中![]() .
.
参考值表:
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】学生学习的自律性很重要.某学校对自律性与学生成绩是否有关进行了调研,从该校学生中随机抽取了100名学生,通过调查统计得到![]() 列联表的部分数据如下表:
列联表的部分数据如下表:
自律性一般 | 自律性强 | 合计 | |
成绩优秀 | 40 | ||
成绩一般 | 20 | ||
合计 | 50 | 100 |
(1)补全![]() 列联表中的数据;
列联表中的数据;
(2)判断是否有![]() 的把握认为学生的自律性与学生成绩有关.
的把握认为学生的自律性与学生成绩有关.
参考公式及数据: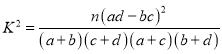 .
.
| 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |