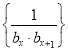题目内容
【题目】对于双曲线![]() :
:![]() (
(![]() ),若点
),若点![]() 满足
满足![]() ,则称
,则称![]() 在
在![]() 的外部;若点
的外部;若点![]() 满足
满足![]() ,则称
,则称![]() 在
在![]() 的内部.
的内部.
(1)若直线![]() 上点都在
上点都在![]() 的外部,求
的外部,求![]() 的取值范围;
的取值范围;
(2)若![]() 过点
过点![]() ,圆
,圆![]() (
(![]() )在
)在![]() 内部及
内部及![]() 上的点构成的圆弧长等于该圆周长的一半,求
上的点构成的圆弧长等于该圆周长的一半,求![]() 、
、![]() 满足的关系式及
满足的关系式及![]() 的取值范围;
的取值范围;
(3)若曲线![]() (
(![]() )上的点都在
)上的点都在![]() 的外部,求
的外部,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() ,
,![]() ;(3)
;(3)![]() .
.
【解析】
(1)直线![]() 上点都在
上点都在![]() 的外部等价于不等式
的外部等价于不等式![]() 的解为一切实数,转化为恒成立问题从而求解;
的解为一切实数,转化为恒成立问题从而求解;
(2)根据对称性,只需要考虑这两个曲线在第一象限及![]() 、
、![]() 轴正半轴的情况,由此可得两曲线的交点坐标为
轴正半轴的情况,由此可得两曲线的交点坐标为![]() ,将点
,将点![]() 和
和![]() 代入双曲线得到两个方程,然后将
代入双曲线得到两个方程,然后将![]() 看成已知数,解出
看成已知数,解出![]() ,根据
,根据![]() ,解出
,解出![]() 的范围;
的范围;
(3)先将曲线![]() (
(![]() )转化为
)转化为![]() ,根据所有点都在
,根据所有点都在![]() 的外部,可以得到不等式
的外部,可以得到不等式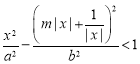 对任意非零实数
对任意非零实数![]() 均成立,令
均成立,令![]() ,转化为函数进行分类讨论,求解最值,从而得出
,转化为函数进行分类讨论,求解最值,从而得出![]() 的取值范围.
的取值范围.
解:(1)由题意,因为直线![]() 上点都在
上点都在![]() 的外部,
的外部,
所以直线![]() 上点
上点![]() 满足
满足![]() ,
,
即求不等式![]() 的解为一切实数时
的解为一切实数时![]() 的取值范围.
的取值范围.
对于不等式![]() ,
,
当![]() 时,不等式的解集不为一切实数,
时,不等式的解集不为一切实数,
于是有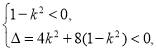 解得
解得![]() .
.
故![]() 的取值范围为
的取值范围为![]() .
.
(2)因为圆![]() 和双曲线
和双曲线![]() 均关于坐标轴和原点对称,
均关于坐标轴和原点对称,
所以只需考虑这两个曲线在第一象限及![]() 、
、![]() 轴正半轴的情况.
轴正半轴的情况.
由题设,圆与双曲线的交点平分该圆在第一象限内的圆弧,
它们交点的坐标为![]() .
.
将![]() ,
,![]() 代入双曲线
代入双曲线![]() 方程,
方程,
得![]() (*),
(*),
又因为![]() 过点
过点![]() ,
,
所以![]() ,
,
将![]() 代入(*)式,
代入(*)式,
得![]() .
.
由![]() ,
,
解得![]() .
.
因此,![]() 的取值范围为
的取值范围为![]() .
.
(3)由![]() ,
,
得![]() .
.
将![]() 代入
代入![]() ,
,
因为曲线![]() (
(![]() )上的点都在
)上的点都在![]() 的外部,
的外部,
所以不等式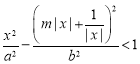 对任意非零实数
对任意非零实数![]() 均成立,
均成立,
其中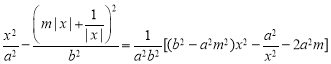 .
.
令![]() ,设
,设![]() ,(
,(![]() ).
).
当![]() 时,函数
时,函数![]() 在
在![]() 上单调递增,
上单调递增,![]() 不恒成立;
不恒成立;
当![]() 时,
时,![]() ,
,
函数![]() 的最大值为
的最大值为![]() ,
,
因为![]() ,所以
,所以![]() ;
;
当![]() 时,
时,![]() .
.
综上,![]() ,解得
,解得![]() .
.
因此,![]() 的取值范围为
的取值范围为![]() .
.

 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案【题目】某饼屋进行为期![]() 天的五周年店庆活动,现策划两项有奖促销活动,活动一:店庆期间每位顾客一次性消费满
天的五周年店庆活动,现策划两项有奖促销活动,活动一:店庆期间每位顾客一次性消费满![]() 元,可得
元,可得![]() 元代金券一张;活动二:活动期间每位顾客每天有一次机会获得一个一元或两元红包.根据前一年该店的销售情况,统计了
元代金券一张;活动二:活动期间每位顾客每天有一次机会获得一个一元或两元红包.根据前一年该店的销售情况,统计了![]() 位顾客一次性消费的金额数(元),频数分布表如下图所示:
位顾客一次性消费的金额数(元),频数分布表如下图所示:
一次性消费金额数 |
|
|
|
|
|
人数 |
|
|
|
|
|
以这![]() 位顾客一次消费金额数的频率分布代替每位顾客一次消费金额数的概率分布.
位顾客一次消费金额数的频率分布代替每位顾客一次消费金额数的概率分布.
(1)预计该店每天的客流量为![]() 人次,求这次店庆期间,商家每天送出代金券金额数的期望;
人次,求这次店庆期间,商家每天送出代金券金额数的期望;
(2)假设顾客获得一元或两元红包的可能性相等,商家在店庆活动结束后会公布幸运数字,连续![]() 元的“店庆幸运红包”一个.若公布的幸运数字是“
元的“店庆幸运红包”一个.若公布的幸运数字是“![]() ”,求店庆期间一位连续
”,求店庆期间一位连续![]() 天消费的顾客获得红包金额总数的期望.
天消费的顾客获得红包金额总数的期望.