题目内容
定义域为 的函数
的函数 满足
满足 当
当 时,
时, ,若
,若 时,
时, 恒成立,则实数
恒成立,则实数 的取值范围是( )
的取值范围是( )
A.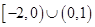 | B. |
C. | D. |
C
解析试题分析:当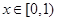 时,
时,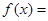
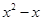 ,
,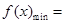
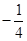 ;当
;当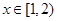 时,
时,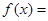
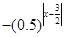 ,
,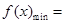
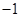 ,当
,当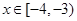 时,
时,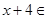
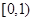 ,
,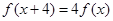 ,
,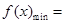
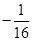 ;当
;当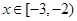 时,
时,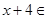
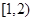 ,
,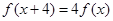 ,
,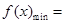
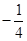 ,综上所述
,综上所述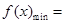
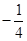 ,故
,故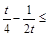
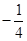 ,解得
,解得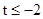 或
或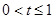 ,故选C.
,故选C.
考点:1.分段函数;2.二次函数的性质;3.指数函数的性质.

练习册系列答案
相关题目
已知函数 与
与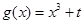 ,若
,若 与
与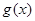 的交点在直线
的交点在直线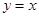 的两侧,
的两侧,
则实数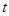 的取值范围是 ( )
的取值范围是 ( )
A.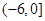 | B.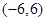 | C.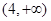 | D.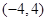 |
若不等式 对任意不大于1的实数x和大于1的正整数n都成立,则
对任意不大于1的实数x和大于1的正整数n都成立,则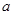 的取值范围是( )
的取值范围是( )
A.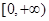 | B.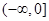 | C.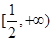 | D.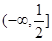 |
 的零点所在区间为( )
的零点所在区间为( )
| A.(0,1) | B.(-1,0) | C.(1,2) | D.(-2,-l) |
若 ,则
,则 ()
()
A.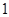 | B. | C. | D.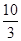 |
设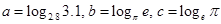 ,则( )
,则( )
A. | B. | C. | D. |
若 ,则有( ).
,则有( ).
A.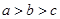 | B. | C. | D. |
某家具的标价为132元,若降价以九折出售(即优惠10%),仍可获利10%(相对进货价),则该家具的进货价是( )
| A.118元 | B.105元 |
| C.106元 | D.108元 |
 万元购进一台新设备用于生产. 第一年需运营费用
万元购进一台新设备用于生产. 第一年需运营费用 万元,从第二年起,每年运营费用均比上一年增加
万元,从第二年起,每年运营费用均比上一年增加 万元. 设该设备使用了
万元. 设该设备使用了 年后,盈利总额达到最大值(盈利额等于收入减去成本),则
年后,盈利总额达到最大值(盈利额等于收入减去成本),则 等于( )
等于( )


