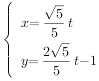题目内容
【题目】已知函数f（x）= 
，g（x）=f（x）﹣a
（1）当a=2时，求函数g（x）的零点；
（2）若函数g（x）有四个零点，求a的取值范围；
（3）在（2）的条件下，记g（x）得四个零点分别为x1 ， x2 ， x3 ， x4 ， 求x1+x2+x3+x4的取值范围．
【答案】
（1）解：当x＞0时，由|lnx|=2解得x=e2或x= 
，
当x≤0时，由x2+4x+1=2解得x=﹣2+ 
（舍）或x=﹣2﹣ ，
∴函数g（x）有三个零点，分别为x=e2或x= ，x=﹣2﹣ ．
（2）解：函数g（x）=f（x）﹣a的零点个数即f（x）的图象与c的图象的交点个数，
作函数f（x）的图象y=a的图象，结合两函数图象可知，
函数g（x）有四个零点时a的取值范围是0＜a≤1；
（3）解：不妨设x1＜x2＜x3＜x4，结合图象知x1+x2=﹣4且0＜x3＜1，x4＞1，
由|lnx3|=|lnx4|=a，知x3x4=1且x4∈（1，e]，
∴x3+x4= 
+x4∈（2，e+ 
]，
故x1+x2+x3+x4的取值范围是∈（﹣2，e+ ﹣4]
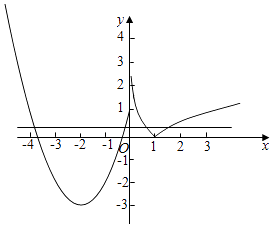
【解析】（1）根据函数零点的定义解方程即可．（2）利用函数与方程之间的关系转化为两个函数的交点个数问题，利用数形结合进行判断求解．（3）根据函数图象结合函数的对称性进行判断即可．
练习册系列答案
相关题目
