题目内容
14.已知函数f(x)=sin(ωx+φ)[ω>0,0<φ<$\frac{π}{2}$]的图象经过点(0,$\frac{1}{2}$),且相邻两条对称轴的距离为$\frac{π}{2}$,求函数f(x)的解析式及其在[0,π]上的单增区间.分析 根据图象求出A,T,求出ω,图象经过(0,$\frac{1}{2}$),求出φ,然后求f(x)的解析式,再根据正弦函数的图象得到在[0,π]上的单增区间.
解答 解:∵相邻两条对称轴的距离为$\frac{π}{2}$,
∴$\frac{1}{2}$T=$\frac{π}{2}$,
∴T=π,
∴ω=$\frac{2π}{π}$=2,
∴f(x)=sin(2x+φ),
∵图象经过点(0,$\frac{1}{2}$),
∴f(0)=sinφ=$\frac{1}{2}$,
∵0<φ<$\frac{π}{2}$,
∴φ=$\frac{π}{6}$,
∴f(x)=sin(2x+$\frac{π}{6}$),
∴单调增区间为2kπ-$\frac{π}{2}$≤2x+$\frac{π}{6}$≤2kπ+$\frac{π}{2}$,
∴kπ-$\frac{π}{3}$≤x≤kπ+$\frac{π}{6}$,
当k=0时,-$\frac{π}{3}$≤x≤$\frac{π}{6}$,
当k=1时,$\frac{2π}{3}$≤x≤$\frac{7π}{6}$,
∴在[0,π]上的单增区间为[0,$\frac{π}{6}$],[$\frac{2π}{3}$,π].
点评 本题考查由y=Asin(ωx+φ)的部分图象确定其解析式,着重考查正弦函数的单调性,考查运算求解能力,属于中档题

练习册系列答案
相关题目
20.在△ABC中,角A,B,C的对边分别是a,b,c,若$\frac{a}{sinB}+\frac{b}{sinA}=2c$,则∠A的大小是( )
| A. | $\frac{π}{2}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{6}$ |
6.已知$\frac{1}{m}$+$\frac{2}{n}$=1(m>0,n>0),当mn取最小值时,双曲线$\frac{x^2}{m^2}$-$\frac{y^2}{mn}$=1的离心率为( )
| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $\frac{1}{2}$ | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
3.执行如图所示的程序框图,则输出的n的值是( )
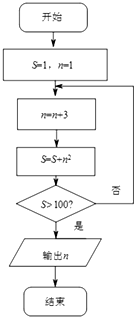

| A. | 7 | B. | 10 | C. | 66 | D. | 166 |
 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1的左顶点为A(-3,0),左焦点恰为圆x2+2x+y2+m=0(m∈R)的圆心M.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1的左顶点为A(-3,0),左焦点恰为圆x2+2x+y2+m=0(m∈R)的圆心M.