题目内容
设集合P={x|sinx=1,x∈R},Q={x|cosx=-1,x∈R},则( )
| A、P∩Q=∅ | ||
| B、P⊆Q | ||
C、P∪Q={x|x=
| ||
| D、P=Q |
分析:根据 集合P={x|sinx=1,x∈R}={x|x=2kπ+
,k∈z},
Q={x|cosx=-1,x∈R}={x|x=2kπ+π,k∈z},从而得到 P∩Q=∅.
| π |
| 2 |
Q={x|cosx=-1,x∈R}={x|x=2kπ+π,k∈z},从而得到 P∩Q=∅.
解答:解:集合P={x|sinx=1,x∈R}={x|x=2kπ+
,k∈z},
Q={x|cosx=-1,x∈R}={x|x=2kπ+π,k∈z},故 P∩Q=∅,
故选 A.
| π |
| 2 |
Q={x|cosx=-1,x∈R}={x|x=2kπ+π,k∈z},故 P∩Q=∅,
故选 A.
点评:本题考查集合的表示方法,两个集合的交集的定义和求法,根据三角函数的值求角,求出P和Q,是解题的关键.

练习册系列答案
相关题目
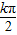 ,k∈Z}
,k∈Z}