题目内容
16.已知函数f(x)=$\frac{{x}^{2}}{lnx}$(1)求f(x)的单调区间;
(2)证明:x>1时,x+(x-3)e${\;}^{\frac{x}{2}}$lnx>0.
分析 (1)先求出函数的导数,通过解关于导函数的不等式,从而求出函数f(x)的单调区间;
(2)通过求导得到g(x)的单调性,进而有g(x)≤g(2),推出x>1时,f(x)>g(x),从而证出结论.
解答 解:(1)∵f(x)=$\frac{{x}^{2}}{lnx}$,定义域为:(0,1)∪(1,+∞),
∴f′(x)=$\frac{x(2lnx-1)}{{(lnx)}^{2}}$,
由f′(x)>0,解得:x>$\sqrt{e}$,由f′(x)<0,解得:0<x<1或1<x<$\sqrt{e}$,
∴f(x)在($\sqrt{e}$,+∞)单调递增,在(0,1)和(1,$\sqrt{e}$)单调递减;
(2)由(1)知:当x>1时,f(x)最小值=f($\sqrt{e}$)=$\frac{e}{ln\sqrt{e}}$=2e,
令g(x)=(-x2+3x)${e}^{\frac{x}{2}}$,x∈(1,+∞),则g′(x)=-$\frac{1}{2}$(x-2)(x+3)${e}^{\frac{x}{2}}$,
由g′(x)>0得g(x)在(1,2)单调递增,
由g′(x)<0得g(x)在(2,+∞)单调递减,
∴g(x)≤g(2)=2e,
∴x>1时,f(x)>g(x),
即x+(x-3)e${\;}^{\frac{x}{2}}$lnx>0.
点评 本题考查了利用导数研究函数的单调性极值与最值、问题的等价转化方法、分类讨论思想方法,考查了推理能力与计算能力,属于难题.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
11.如图,水平放置的几何体的三视图,其俯视图为图中含有实线和虚线的矩形,侧(左)视图为边长为3,高为$\sqrt{3}$的矩形,则该几何体的表面积为( )
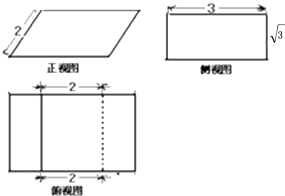

| A. | 30+6$\sqrt{3}$ | B. | 6+15$\sqrt{3}$ | C. | 21$\sqrt{3}$ | D. | 42 |
6.设ω>0,函数f(x)=sin(ωx+$\frac{π}{4}$)的图象向左平移$\frac{π}{8}$个单位后,图象关于y轴对称,则ω的最小值为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 2 | D. | 4 |
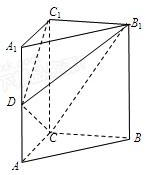 如图,直三棱柱ABC-A1B1C1中,点D在棱AA1上,且∠ACB=90°,AA1=BC=2,AC=1.
如图,直三棱柱ABC-A1B1C1中,点D在棱AA1上,且∠ACB=90°,AA1=BC=2,AC=1.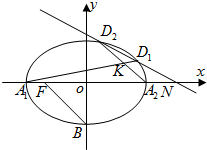 如图,椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{{\sqrt{2}}}{2}$,B、F分别为其短轴的一个端点和左焦点,且|BF|=$\sqrt{2}$.
如图,椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{{\sqrt{2}}}{2}$,B、F分别为其短轴的一个端点和左焦点,且|BF|=$\sqrt{2}$.