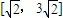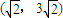题目内容
已知
、
是夹角为60°的两个单位向量,则
=2
+
和b=-3
+2
的夹角是( )
| m |
| n |
| a |
| m |
| n |
| m |
| n |
分析:由题意可得|
|=|
|=1,
•
=
.设
=2
+
和b=-3
+2
的夹角为θ,0°≤θ≤180°,可得
•
=-
.再求得|
|和|
|,根据
•
=
=-
,可得 θ 的值.
| m |
| n |
| m |
| n |
| 1 |
| 2 |
| a |
| m |
| n |
| m |
| n |
| a |
| b |
| 7 |
| 2 |
| a |
| b |
| a |
| b |
| ||||
|
|
| 1 |
| 2 |
解答:解:由题意可得|
|=|
|=1,
•
=1×1×cos60°=
.
设
=2
+
和b=-3
+2
的夹角为θ,0°≤θ≤180°,可得
•
=(2
+
)•(-3
+2
)=-6
2+2
2+
•
=-
.
再由|
|=
=
=
,|
|=
=
=
,
∴
•
=
=
=-
,∴θ=120°,
故选C.
| m |
| n |
| m |
| n |
| 1 |
| 2 |
设
| a |
| m |
| n |
| m |
| n |
| a |
| b |
| m |
| n |
| m |
| n |
| m |
| n |
| m |
| n |
| 7 |
| 2 |
再由|
| a |
|
4
|
| 7 |
| b |
|
9
|
| 7 |
∴
| a |
| b |
| ||||
|
|
-
| ||||
|
| 1 |
| 2 |
故选C.
点评:本题主要考查用两个向量的数量积表示两个向量的夹角,两个向量数量积的定义,属于中档题.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
已知向量
=(m-1,n-1),
=(m-3,n-3)且
与
的夹角为钝角,则m+n的取值范围是( )
| a |
| b |
| a |
| b |
| A、[2,6] | ||||
B、[
| ||||
C、(
| ||||
| D、(2,6) |
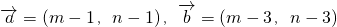 且
且 与
与 的夹角为钝角,则m+n的取值范围是
的夹角为钝角,则m+n的取值范围是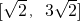
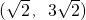
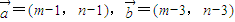 且
且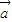 与
与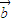 的夹角为钝角,则m+n的取值范围是( )
的夹角为钝角,则m+n的取值范围是( )