题目内容
(2013•安徽)在平面直角坐标系中,O是坐标原点,两定点A,B满足
=
=
•
=2,则点集{P|
=λ
+μ
,
+
≤1,λ、μ∈R}所表示的区域面积是( )
|
|
| OA |
| OB |
| OP |
| OA |
| OB |
|
|
分析:由两定点A,B满足
=
=
•
=2,说明O,A,B三点构成边长为2的等边三角形,设出两个定点的坐标,再设出P点坐标,由平面向量基本定理,把P的坐标用A,B的坐标及λ,μ表示,把不等式|λ|+|μ|≤1去绝对值后可得线性约束条件,画出可行域可求点集P所表示区域的面积.
|
|
| OA |
| OB |
解答:解:由两定点A,B满足
=
=
•
=2,说明O,A,B三点构成边长为2的等边三角形.
不妨设A(
,-1),B(
,1).再设P(x,y).
由
=λ
+μ
,得:(x,y)=(
λ,-λ)+(
μ,μ)=(
(λ+μ),μ-λ).
所以
,解得
①.
由|λ|+|μ|≤1.
所以①等价于
或
或
或
.
可行域如图中矩形ABCD及其内部区域,
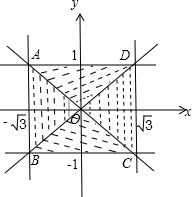
则区域面积为2×2
=4
.
故选D.
|
|
| OA |
| OB |
不妨设A(
| 3 |
| 3 |
由
| OP |
| OA |
| OB |
| 3 |
| 3 |
| 3 |
所以
|
|
由|λ|+|μ|≤1.
所以①等价于
|
|
|
|
可行域如图中矩形ABCD及其内部区域,

则区域面积为2×2
| 3 |
| 3 |
故选D.
点评:本题考查了平面向量的基本定理及其意义,考查了二元一次不等式(组)所表示的平面区域,考查了数学转化思想方法,解答此题的关键在于读懂题意,属中档题.

练习册系列答案
 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案
相关题目