题目内容
厂家在产品出厂前,需对产品做检验,厂家将一批产品发给商家时,商家按合同规定也需随机抽取一定数量的产品做检验,以决定是否接收这批产品.(Ⅰ)若厂家库房中的每件产品合格的概率为0.8,从中任意取出4件进行检验.求至少有1件是合格品的概率;
(Ⅱ)若厂家发给商家20件产品,其中有3件不合格,按合同规定该商家从中任取2件,都进行检验,只有2件都合格时才接收这批产品,否则拒收.求该商家可能检验出不合格产品数ξ的分布列及期望Eξ,并求该商家拒收这批产品的概率.
分析:(1)由对立事件概率公式,及产品合格的概率为0.8,我们易得从产品中任意取出4件进行检验.求至少有1件是合格品的概率;
(2)根据(1)的结论,根据分布列及数学期望的计算公式,易得到最终结果.
(2)根据(1)的结论,根据分布列及数学期望的计算公式,易得到最终结果.
解答:解:(Ⅰ)记“厂家任取4件产品检验,其中至少有1件是合格品”为事件A
用对立事件A来算,有P(A)=1-P(
)=1-0.24=0.9984
(Ⅱ)ξ可能的取值为0,1,2
P(ξ=0)=
=
,
P(ξ=1)=
=
,
P(ξ=2)=
=
Eξ=0×
+1×
+2×
=
记“商家任取2件产品检验,都合格”为事件B,
则商家拒收这批产品的概率P=1-P(B)=1-
=
所以商家拒收这批产品的概率为
.
用对立事件A来算,有P(A)=1-P(
. |
| A |
(Ⅱ)ξ可能的取值为0,1,2
P(ξ=0)=
| ||
|
| 136 |
| 190 |
P(ξ=1)=
| ||||
|
| 51 |
| 190 |
P(ξ=2)=
| ||
|
| 3 |
| 190 |
| ξ | 0 | 1 | 2 | ||||||
| P |
|
|
|
| 136 |
| 190 |
| 51 |
| 190 |
| 3 |
| 190 |
| 3 |
| 10 |
记“商家任取2件产品检验,都合格”为事件B,
则商家拒收这批产品的概率P=1-P(B)=1-
| 136 |
| 190 |
| 27 |
| 95 |
所以商家拒收这批产品的概率为
| 27 |
| 95 |
点评:本题所考查的知识点难度不高,理解起来很容易,思路也较清晰,但由于解题思路受题目中游戏规则的限制,故解决本题的关键是仔细分析题意,特别是计分规则,及每种分值产生的情况,不要有重复和遗漏,否则对结果,特别是分布列和数学期望的计算产生重大的影响.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
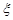 的分布列及期望
的分布列及期望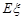 ,并求该商家拒收这批产品的概率.
,并求该商家拒收这批产品的概率.