题目内容
厂家在产品出厂前,需对产品做检验,商家按合同规定也需随机抽样做检验,以决定是否接收这批产品.
(1)厂家在一批数量很大的产品中进行抽检,若每件产品合格的概率为
,从中任意取出3件进行检验,求可能检验出不合格产品数X的分布列;
(2)若厂家发给商家20件产品,其中有3件不合格.按合同规定该商家从中任取2件,都进行检验,只有2件都合格时才接收这批产品,否则拒收.求该商家可能检验出不合格产品数Y的分布列,并求该商家拒收这批产品的概率.
(1)厂家在一批数量很大的产品中进行抽检,若每件产品合格的概率为
| 4 | 5 |
(2)若厂家发给商家20件产品,其中有3件不合格.按合同规定该商家从中任取2件,都进行检验,只有2件都合格时才接收这批产品,否则拒收.求该商家可能检验出不合格产品数Y的分布列,并求该商家拒收这批产品的概率.
分析:(1)可能检验出不合格产品数为X,则X~B(3,
).由此能求出离散型随机变量X的分布列.
(2)可能检验出不合格产品数为Y,则Y服从超几何分布,所以有p(Y=0)=
=
,P(Y=1)=
=
,P(Y=3)=
=
.由此能求出离散型随机变量Y的分布列和商家拒收这批产品的概率.
| 1 |
| 5 |
(2)可能检验出不合格产品数为Y,则Y服从超几何分布,所以有p(Y=0)=
| ||
|
| 136 |
| 190 |
| ||||
|
| 51 |
| 190 |
| ||
|
| 3 |
| 190 |
解答:(1)解:可能检验出不合格产品数为X,则X~B(3,
).
P(X=0)=
(
)3(
)0=
,
P(X=1)=
(
) 2(
)1=
,
P(X=2)=
(
)1(
)2=
,
p(X=3)=
(
) 0(
) 3=
.
则离散型随机变量X的分布列为:
(2)可能检验出不合格产品数为Y,则Y服从超几何分布,所以有:
p(Y=0)=
=
,
P(Y=1)=
=
,
P(Y=3)=
=
.
则离散型随机变量Y的分布列为:
由题意,商家拒收这批产品的概率为:P(Y≥1)=1-P(Y=0)=
.
| 1 |
| 5 |
P(X=0)=
| C | 0 3 |
| 4 |
| 5 |
| 1 |
| 5 |
| 64 |
| 125 |
P(X=1)=
| C | 1 3 |
| 4 |
| 5 |
| 1 |
| 5 |
| 48 |
| 125 |
P(X=2)=
| C | 2 3 |
| 4 |
| 5 |
| 1 |
| 5 |
| 12 |
| 125 |
p(X=3)=
| C | 3 3 |
| 4 |
| 5 |
| 1 |
| 5 |
| 1 |
| 125 |
则离散型随机变量X的分布列为:
| X | 0 | 1 | 2 | 3 | ||||||||
| P |
|
|
|
|
p(Y=0)=
| ||
|
| 136 |
| 190 |
P(Y=1)=
| ||||
|
| 51 |
| 190 |
P(Y=3)=
| ||
|
| 3 |
| 190 |
则离散型随机变量Y的分布列为:
| Y | 0 | 1 | 2 | ||||||
| P |
|
|
|
| 27 |
| 95 |
点评:本题考查离散型随机变量的分布列和数学期望,考查学生的运算能力,考查学生探究研究问题的能力,解题时要认真审题,理解古典概型的特征:试验结果的有限性和每一个试验结果出现的等可能性,体现了化归的重要思想.注意二项分布和超几何分布的性质和应用.

练习册系列答案
相关题目
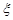 的分布列及期望
的分布列及期望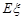 ,并求该商家拒收这批产品的概率.
,并求该商家拒收这批产品的概率.