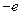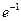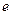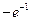题目内容
函数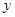 =
=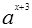 -2的图象恒过定点A,且点A在直线
-2的图象恒过定点A,且点A在直线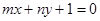 上(
上(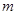 >0,
>0,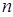 >0),则
>0),则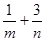 的最小值为( )
的最小值为( )
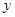 =
=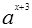 -2的图象恒过定点A,且点A在直线
-2的图象恒过定点A,且点A在直线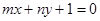 上(
上(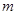 >0,
>0,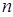 >0),则
>0),则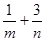 的最小值为( )
的最小值为( ) | A.12 | B.10 | C.8 | D.14 |
A
分析:根据y=ax过定点(0,1)求出点A的坐标,再把点A代入直线方程得到3m+n=1,再把“1”整体代入所求的式子,利用基本不等式求出最小值.
解:∵函数y=ax+3-2的图象恒过定点A,∴A(-3,-1),
∵点A在直线mx+ny+1=0上,∴3m+n=1,
∵m>0,n>0,
∴
 +
+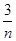 =(
=( +
+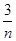 )(3m+n)=6+
)(3m+n)=6+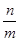 +
+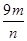 ≥6+6=12,当且仅当
≥6+6=12,当且仅当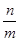 =
=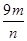 时取等号,
时取等号,∴所求的最小值是12,
故选A.

练习册系列答案
相关题目
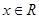 ,f’(x)>2,则f(x)>2x+4的解集为( )
,f’(x)>2,则f(x)>2x+4的解集为( )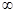 )
) ,
,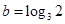 ,
,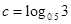 ,则( )
,则( )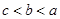
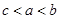
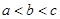
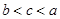
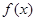 满足:对任意
满足:对任意 ,且
,且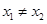 ,都有
,都有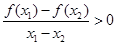 ,则( )
,则( )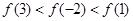
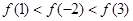
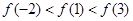
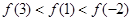
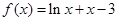 的零点
的零点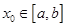 ,且
,且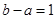 ,
,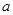 ,
,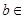 N*,
N*,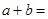 ( )
( )
 的解为 ▲ .
的解为 ▲ .
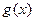 的图象与
的图象与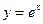 图象关于直线
图象关于直线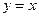 对称,函数
对称,函数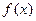 与
与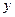 轴对称,若
轴对称,若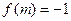 ,则
,则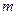 的值是( )
的值是( )