题目内容
(本小题12分)设函数
(1)求函数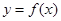 的单调区间;
的单调区间;
(2)求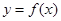 在
在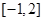 上的最小值;
上的最小值;
【答案】
(1)函数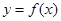 的增区间为
的增区间为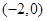 和
和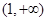 ,减区间为
,减区间为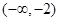 和
和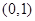 .
.
(2) 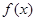 在
在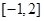 上的最小值为
上的最小值为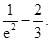
【解析】本试题主要是考查了导数在研究函数中的 运用。求解函数的单调性以及函数的最值的综合运用。
(1)首先分析定义域,然后求解导数,令导数为零,得到导函数与x轴 的交点,然后分析导数大于零或者小于零的解得到结论。
(2)根据第一问的结论,结合函数的单调性,可知函数在给定区间的最值问题。
解:(1)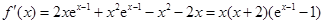 ,
,
令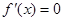 ,可得
,可得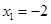 ,
,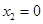 ,
,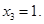
当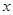 变化时,
变化时,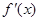 ,
,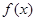 的变化情况如下表:
的变化情况如下表:
|
|
|
|
|
0 |
|
1 |
|
|
|
- |
0 |
+ |
0 |
- |
0 |
+ |
|
|
|
极小值 |
|
极大值 |
|
极小值 |
|
 函数
函数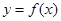 的增区间为
的增区间为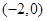 和
和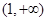 ,减区间为
,减区间为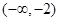 和
和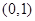 .
.
(2)当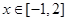 时,
时,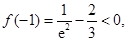
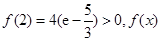 极小值
极小值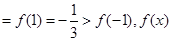 极大值
极大值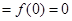 .
.
所以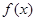 在
在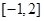 上的最小值为
上的最小值为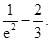

练习册系列答案
相关题目
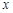
 的部分图象如图所示:
的部分图象如图所示: 的值;
的值; ,当
,当 时,求函数
时,求函数 的值域.
的值域.

