题目内容
（5分）（2011•广东）正五棱柱中，不同在任何侧面且不同在任何底面的两顶点的连线称为它的对角线，那么一个正五棱柱对角线的条数共有（ ）
| A．20 | B．15 | C．12 | D．10 |
D
解析试题分析：抓住上底面的一个顶点，看从此顶点出发的对角线有多少条即可解决．
解：由题意正五棱柱对角线一定为上底面的一个顶点和下底面的一个顶点的连线，因为不同在任何侧面内，
故从一个顶点出发的对角线有2条．正五棱柱对角线的条数共有2×5=10条．
故选D
点评：本题考查计数原理在立体几何中的应用，考查空间想象能力．
练习册系列答案
相关题目
教育部直属师范大学免费师范毕业生一般回生源所在省份中小学校任教. 今年春节后，我校迎来了陕西师范大学数学系5名实习教师，若将5名实习教师分配到高一年级的3个班实习，每班至少1名，最多2名，则不同的分配方案有（ ）
| A．60种 | B．90种 | C．120种 | D．180种 |
若
.则
( )
| A．20 | B．19 | C． | D． |
如果小明在某一周的第一天和第七天分别吃了3个水果，且从这周的第二天开始，每天所吃水果的个数与前一天相比，仅存在三种可能：或“多一个”或“持平”或“少一个”，那么，小明在这一周中每天所吃水果个数的不同选择方案共有（ ）
A． 种 | B． 种 | C． 种 | D． 种 |
设
，使
的展开式中含有常数项的最小的
为（ ）
| A．4 | B．5 | C．6 | D．7 |
某搬运工不慎将4件次品与6件正品混在一起，由于产品外观一样，需要用仪器对产品一一检测，直至找到所有次品为止，若至多检测6次就能找到所有次品，则不同的检测方法共有（ ）种.
| A．1950 | B．2130 | C．7800 | D．8520 |
[2014·衡阳质检]4位同学每人从甲、乙、丙3门课程中选修1门，则恰有2人选修课程甲的不同选法共有( )
| A．12种 | B．24种 | C．30种 | D．36种 |
一排9个座位坐了3个三口之家，若每家人坐在一起，则不同的坐法种是为（ ）
A． | B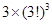． | C． | D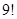． |