题目内容
已知△ 的内角
的内角 所对的边分别为
所对的边分别为 且
且 .
.
(1) 若 , 求
, 求 的值;
的值;
(2) 若△ 的面积
的面积 求
求 的值.
的值.
 的内角
的内角 所对的边分别为
所对的边分别为 且
且 .
.(1) 若
 , 求
, 求 的值;
的值;(2) 若△
 的面积
的面积 求
求 的值.
的值.(1) 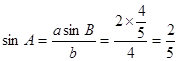 .
.
(2)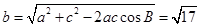
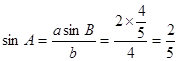 .
. (2)
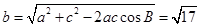
本小题主要考查正弦定理、余弦定理、同角三角函数的基本关系等基础知识,考查运算求解能力。第一问中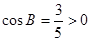 ,得到正弦值
,得到正弦值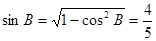 ,再结合正弦定理可知,
,再结合正弦定理可知,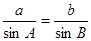 ,得到
,得到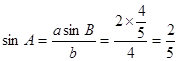 (2)中
(2)中 即
即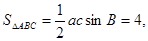 所以c=5,再利用余弦定理
所以c=5,再利用余弦定理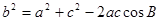 ,得到b的值。
,得到b的值。
解: (1)∵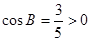 , 且
, 且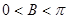 , ∴
, ∴ 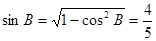 . 由正弦定理得
. 由正弦定理得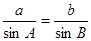 , ∴
, ∴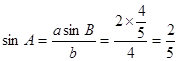 .
.
(2)∵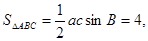 ∴
∴ . ∴c=5
. ∴c=5
由余弦定理得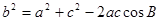 ,
,
∴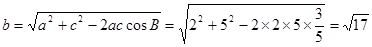
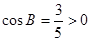 ,得到正弦值
,得到正弦值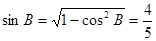 ,再结合正弦定理可知,
,再结合正弦定理可知,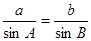 ,得到
,得到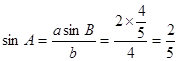 (2)中
(2)中 即
即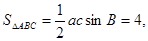 所以c=5,再利用余弦定理
所以c=5,再利用余弦定理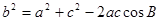 ,得到b的值。
,得到b的值。解: (1)∵
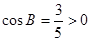 , 且
, 且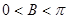 , ∴
, ∴ 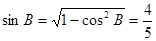 . 由正弦定理得
. 由正弦定理得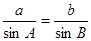 , ∴
, ∴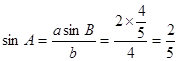 .
. (2)∵
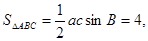 ∴
∴ . ∴c=5
. ∴c=5 由余弦定理得
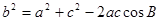 ,
,∴
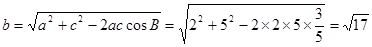

练习册系列答案
相关题目
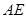 的高度
的高度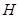 (单位
(单位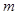 ),如示意图,垂直放置的标杆
),如示意图,垂直放置的标杆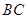 高度
高度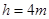 ,仰角
,仰角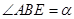 ,
,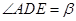 .
.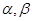 的值,
的值,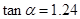 ,
,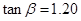 ,请据此算
,请据此算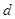 (单位
(单位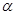 与
与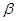 之差较大,可以提高测量精确度,若电视塔实际高度为
之差较大,可以提高测量精确度,若电视塔实际高度为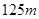 ,问
,问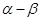 最大?
最大?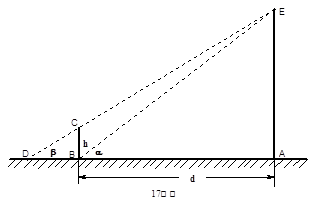
 ,则三角形ABC是( )
,则三角形ABC是( ) ,把y表示成
,把y表示成 的函数关系式;(2)变电站建于何处时,它到三个小区的距离之和最小?
的函数关系式;(2)变电站建于何处时,它到三个小区的距离之和最小?
 中,
中, 、
、 的对边分别是
的对边分别是 、
、 ,且
,且 ,
, ,
, ,那么满足条件的
,那么满足条件的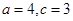 ,则△ABC的面积等于 .
,则△ABC的面积等于 . 中,角
中,角 的对边分别是
的对边分别是 ,若
,若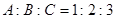 ,则
,则 等于:( )
等于:( )


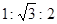
 ,∠A=30°,则∠B等于
,∠A=30°,则∠B等于  中,若
中,若 ,则
,则

