题目内容
用数学归纳法证明:“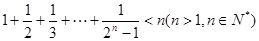 ”时,由
”时,由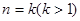 不等式成立,推证
不等式成立,推证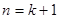 时,左边应增加的项数是( )
时,左边应增加的项数是( )
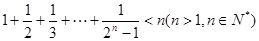 ”时,由
”时,由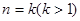 不等式成立,推证
不等式成立,推证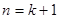 时,左边应增加的项数是( )
时,左边应增加的项数是( )A.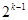 | B.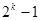 | C.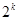 | D.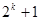 |
C
解:因为用数学归纳法证明:“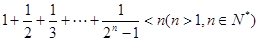 ”时,由
”时,由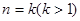 不等式成立,等式左边有
不等式成立,等式左边有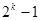 ,因此推证
,因此推证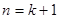 时,左边应
时,左边应 ,因此应该增加的项数是
,因此应该增加的项数是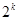 ,选C
,选C
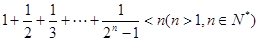 ”时,由
”时,由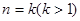 不等式成立,等式左边有
不等式成立,等式左边有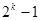 ,因此推证
,因此推证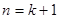 时,左边应
时,左边应 ,因此应该增加的项数是
,因此应该增加的项数是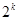 ,选C
,选C
练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
题目内容
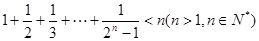 ”时,由
”时,由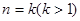 不等式成立,推证
不等式成立,推证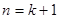 时,左边应增加的项数是( )
时,左边应增加的项数是( )A.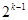 | B.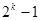 | C.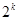 | D.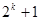 |
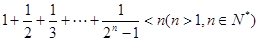 ”时,由
”时,由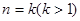 不等式成立,等式左边有
不等式成立,等式左边有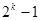 ,因此推证
,因此推证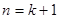 时,左边应
时,左边应 ,因此应该增加的项数是
,因此应该增加的项数是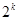 ,选C
,选C
 应用题作业本系列答案
应用题作业本系列答案