题目内容
过点A(2,1)的直线交圆x2+y2-2x+4y=0于B,C两点,当|BC|最大时,直线BC的方程是( )
| A、3x-y-5=0 | B、3x+y-7=0 | C、x+3y-5=0 | D、x-3y+5=0 |
分析:设出直线BC的方程为y=kx+b,由题意可知当|BC|最大时,过A的直线必然过圆的圆心,故把圆的方程化为标准方程,找出圆心的坐标,再由A的坐标,都代入到所设的方程中求出k和b的值,从而确定出直线BC的方程.
解答:解:把圆的方程x2+y2-2x+4y=0化为标准方程为(x-1)2+(y+2)2=5,
∴圆心坐标为(1,-2),
设直线BC的方程为y=kx+b,又A(2,1),
把圆心坐标和A的坐标代入得:
,
解得
,
则直线BC的方程为y=3x-5,即3x-y-5=0.
故选A
∴圆心坐标为(1,-2),
设直线BC的方程为y=kx+b,又A(2,1),
把圆心坐标和A的坐标代入得:
|
解得
|
则直线BC的方程为y=3x-5,即3x-y-5=0.
故选A
点评:此题考查了直线与圆相交的性质,以及根据两点坐标利用待定系数法求直线的解析式,理解|BC|最大即线段BC为圆的直径,即直线BC过圆心是解本题的关键.

练习册系列答案
相关题目

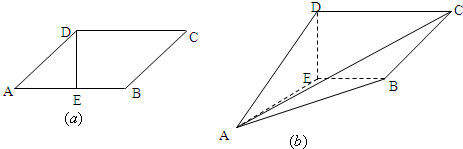 已知边长为2的菱形ABCD,如图(a)所示,∠BAD=60°,过D点作DE⊥AB于E点,现沿着DE折成一个直二面角,如图(b)所示;
已知边长为2的菱形ABCD,如图(a)所示,∠BAD=60°,过D点作DE⊥AB于E点,现沿着DE折成一个直二面角,如图(b)所示; 椭圆E:
椭圆E: 如图,在直三棱柱ABC-A′B′C′中,点D是BC的中点,∠ACB=90°,AC=BC=1,AA′=2,
如图,在直三棱柱ABC-A′B′C′中,点D是BC的中点,∠ACB=90°,AC=BC=1,AA′=2, 过点A(a,0),B(0,b)的直
过点A(a,0),B(0,b)的直 ,原点到该直线的距离为
,原点到该直线的距离为 .
. 求直线MN的方程;
求直线MN的方程; 交椭圆于P、Q两点,以PQ为直径的圆过点D(1,0)?若存在,求出k的值;若不存在,请说明理由。
交椭圆于P、Q两点,以PQ为直径的圆过点D(1,0)?若存在,求出k的值;若不存在,请说明理由。