题目内容
10.已知极坐标的极点在平面直角坐标系的原点O处,极轴与x轴的正半轴重合,且长度单位相同.直线l的极坐标方程为:ρ=$\frac{5}{sin(θ-\frac{π}{3})}$,点P(2cosα,2sinα+2),参数α∈[0,2π].(1)求点P轨迹的直角坐标方程;
(2)求点P到直线l距离的最大值.
分析 (1)设点P(x,y),则$\left\{\begin{array}{l}{x=2cosα}\\{y=2sinα+2}\end{array}\right.$,由此能求出点P的轨迹的直角坐标方程.
(2)由已知得$ρsinθ-\sqrt{3}ρcosθ=10$.从而直线l的直角坐标方程为$\sqrt{3}x-y+10=0$,求出圆心到直线的距离,得点P所在的圆与直线l相离,由此能求出点P到直线l距离的最大值.
解答 解:(1)设点P(x,y),∵P(2cosα,2sinα+2),
∴$\left\{\begin{array}{l}{x=2cosα}\\{y=2sinα+2}\end{array}\right.$,且参数α∈[0,2π],
所以点P的轨迹的直角坐标方程为x2+(y-2)2=4.…(3分)
(2)∵ρ=$\frac{5}{sin(θ-\frac{π}{3})}$,∴$ρsin(θ-\frac{π}{3})$=5,
∴$\frac{1}{2}ρsinθ-\frac{\sqrt{3}}{2}ρcosθ=5$,即$ρsinθ-\sqrt{3}ρcosθ=10$.
∴直线l的直角坐标方程为$\sqrt{3}x-y+10=0$.…(6分)
由(1)知点P的轨迹方程为x2+(y-2)2=4,是圆心为(0,2),半径为2的圆.
圆心到直线的距离d=$\frac{|-2+10|}{\sqrt{(\sqrt{3})^{2}+{1}^{2}}}$=4,
点P所在的圆与直线l相离,…(9分)
∴点P到直线l距离的最大值4+2=6.…(10分)
点评 本题考查极坐标方程与普通方程的互化,考查点到直线距离的最大值的求法,灵活利用极坐标方程与普通方程的互化公式是解决问题的关键.

练习册系列答案
相关题目
20.设a=20.1,b=lg$\frac{5}{2}$,c=log3$\frac{9}{10}$,则a,b,c的大小关系是( )
| A. | b>c>a | B. | a>c>b | C. | b>a>c | D. | a>b>c |
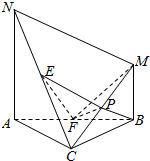 已知△ABC,$AC=BC=\sqrt{2}a$,∠ACB=90°,过点A,B作线段AN,BM分别与△ABC所在的平面垂直,且AN=AB=2BM,E,F,P分别是线段NC,AB,MC的中点.
已知△ABC,$AC=BC=\sqrt{2}a$,∠ACB=90°,过点A,B作线段AN,BM分别与△ABC所在的平面垂直,且AN=AB=2BM,E,F,P分别是线段NC,AB,MC的中点.