Question

【题目】若在曲线(或y=f(x))上两个不同点处的切线重合，则称这条切线为曲线f(x,y)=0或y=f(x)的“自公切线”。
下列方程：
①；
②；
③y=3sinx+4cosx；
④
对应的曲线中存在“自公切线”的有( )
A.①③
B.①④
C.②③
D.②④

Answer 1

【答案】C
【解析】①x2-y2=1 是一个等轴双曲线，没有自公切线；
②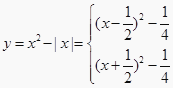 ， 在 x=和 x=- 处的切线都是y=- ， 故②有自公切线．
③=5sin（x+φ），cosφ= ， sinφ= ， 此函数是周期函数，过图象的最高点的切线都重合或过图象的最低点的切线都重合，故此函数有自公切线．
④ ， 即 x2+2|x|+y2-3=0，结合图象可得，此曲线没有自公切线．
所以答案是②③．选C。