题目内容
【题目】全民参与是打赢新型冠状病毒防疫战的根本方法.在防控疫情的过程中，某小区的“卡口”工作人员由“社区工作者”“下沉干部”“志愿者”三种身份的人员构成，其中社区工作者3人，下沉干部2人，志愿者1人.某电视台某天上午随机抽取2人进行访谈，某报社在该天下午随机抽取1人进行访谈.
（1）设
表示上午抽到的社区工作者的人数，求随机变量的分布列和数学期望；
（2）设
为事件“全天抽到的
名工作人员的身份互不相同”，求事件发生的概率.
【答案】（1）详见解析（2）
【解析】
（1）
的可能值为
，分别求出每个值对应的概率，然后做出分布列，进而求出数学期望. （2）身份互不相同为：抽到一名社区工作者，一名下沉干部，一名志愿者.分类讨论逐一计算即可求出概率.
解：（1）的可能值为.
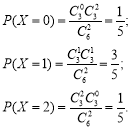（每个）
所以随机变量的分布列为
| 0 | 1 | 2 |
|
|
|
|
（2）身份互不相同为：抽到一名社区工作者，一名下沉干部，一名志愿者，上午同时抽取两个，情况为
，下午抽取一个，情况为
，所以
所以事件
发生的概率.
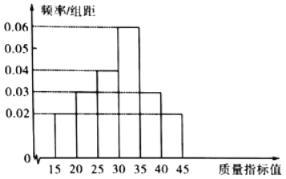
口算题天天练系列答案
【题目】为了提高生产效益，某企业引进了一批新的生产设备，为了解设备生产产品的质量情况，分别从新、旧设备所生产的产品中，各随机抽取100件产品进行质量检测，所有产品质量指标值均在（15，45]以内，规定质量指标值大于30的产品为优质品，质量指标值在（15，30]的产品为合格品.旧设备所生产的产品质量指标值如频率分布直方图所示，新设备所生产的产品质量指标值如频数分布表所示.
质量指标 | 频数 |
（15，20] | 2 |
（20，25] | 8 |
（25，30] | 20 |
（30，35] | 30 |
（35，40] | 25 |
（40，45] | 15 |
合计 | 100 |
（1）请分别估计新、旧设备所生产的产品的优质品率.
（2）优质品率是衡量一台设备性能高低的重要指标，优质品率越高说明设备的性能越高.根据已知图表数据填写下面列联表（单位：件），并判断是否有95%的把握认为“产品质量高与新设备有关”.
非优质品 | 优质品 | 合计 | |
新设备产品 | |||
旧设备产品 | |||
合计 |
附：
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
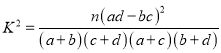，其中
.
（3）用频率代替概率，从新设备所生产的产品中随机抽取3件产品，其中优质品数为X件，求X的分布列及数学期望.
