题目内容
如图所示，四边形ABCD是矩形，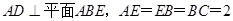
，F为CE上的点，且BF
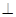平面ACE，AC与BD交于点G
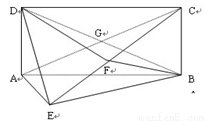
（1）求证：AE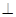平面BCE
（2）求证：AE//平面BFD
【答案】
（1）先证BF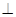
AE （2）先证GF//AE
【解析】
试题分析：（1）∵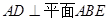 
又知四边形ABCD是矩形，故AD//BC
∴ 
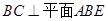故可知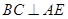 
∵ BF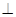平面ACE ∴ BF 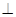AE
又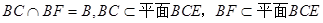 
∴ AE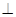平面BCE
（2） 依题意，易知G为AC的中点
又∵ BF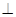平面ACE 所以可知 BF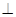EC， 又BE＝EC
∴ 可知F为CE的中点 , 故可知 GF//AE
又可知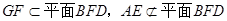 
∴ AE//平面BFD
考点：直线与平面平行的判定；直线与平面垂直的性质；平面与平面垂直的性质．
点评：本题通过线线平行和线面平行，线线垂直和线面垂直及面面垂直的转化，来考查线面、面面平行和垂直的判定定理．
练习册系列答案
阅读快车系列答案
相关题目
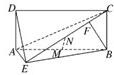如图所示，四边形ABCD为矩形，BC⊥平面ABE，F为CE上的点，且BF⊥平面ACE．
如图所示，四边形PCBM是直角梯形，∠PCB=90°，PM∥BC，PM=PC=AC=1，BC=2，∠ACB=120°，AB⊥PC．
如图所示，四边形ABCD为矩形，AD⊥平面ABE，AE=EB=BC=2，F为CE上的点，且BF⊥平面ACE．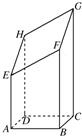
如图所示，以AB=4cm，BC=3cm的长方形ABCD为底面的长方体被平面斜着截断的几何体，EFGH是它的截面．当AE=5cm，BF=8cm，CG=12cm时，试回答下列问题：
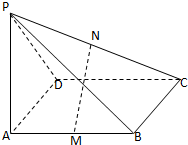如图所示，四边形ABCD是矩形，PA⊥平面ABCD，△PAD是等腰三角形，M、N分别是AB，PC的中点，