题目内容
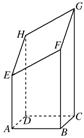
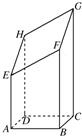 如图所示,以AB=4cm,BC=3cm的长方形ABCD为底面的长方体被平面斜着截断的几何体,EFGH是它的截面.当AE=5cm,BF=8cm,CG=12cm时,试回答下列问题:
如图所示,以AB=4cm,BC=3cm的长方形ABCD为底面的长方体被平面斜着截断的几何体,EFGH是它的截面.当AE=5cm,BF=8cm,CG=12cm时,试回答下列问题:(1)求DH的长;
(2)求这个几何体的体积;
(3)截面四边形EFGH是什么图形?证明你的结论.
分析:(1)过E作EB1⊥BF,垂足为B1,通过平面ABFE∥平面DCGH,说明EF∥HG.过H作HC1⊥CG,垂足为C1,然后求DH的长;
(2)作ED1⊥DH,垂足为D1,B1P⊥CG,垂足为P,连接D1P,B1C1,则几何体被分割成一个长方体ABCD-EB1PD1,一个斜三棱柱EFB1-HGC1,一个直三棱柱EHD1-B1C1P.分别求出体积,即可求这个几何体的体积;
(3)截面四边形EFGH是菱形.先说明EFGH是平行四边形,然后通过计算证明EF=EH.从而证明结论正确.
(2)作ED1⊥DH,垂足为D1,B1P⊥CG,垂足为P,连接D1P,B1C1,则几何体被分割成一个长方体ABCD-EB1PD1,一个斜三棱柱EFB1-HGC1,一个直三棱柱EHD1-B1C1P.分别求出体积,即可求这个几何体的体积;
(3)截面四边形EFGH是菱形.先说明EFGH是平行四边形,然后通过计算证明EF=EH.从而证明结论正确.
解答: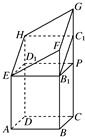 解:(1)过E作EB1⊥BF,垂足为B1,则BB1=AE=5(cm),
解:(1)过E作EB1⊥BF,垂足为B1,则BB1=AE=5(cm),
所以B1F=8-5=3(cm).
因为平面ABFE∥平面DCGH,EF和HG是它们分别与截面的交线,所以EF∥HG.
过H作HC1⊥CG,垂足为C1,
则GC1=FB1=3(cm),
DH=12-3=9(cm).
(2)作ED1⊥DH,垂足为D1,B1P⊥CG,垂足为P,连接D1P,B1C1,则几何体被分割成一个长方体ABCD-EB1PD1,一个斜三棱柱EFB1-HGC1,一个直三棱柱EHD1-B1C1P.从而几何体的体积为
V=3×4×5+
×3×4×3+
×3×4×4=102(cm3).
(3)是菱形.
证明:由(1)知EF∥HG,同理EH∥FG.于是EFGH是平行四边形.
因为EF=
=
=5(cm),
DD1=AE=5(cm),ED1=AD=3(cm),
HD1=4(cm),
所以EH=
=
.=5(cm).
所以EF=EH.
故EFGH是菱形.
 解:(1)过E作EB1⊥BF,垂足为B1,则BB1=AE=5(cm),
解:(1)过E作EB1⊥BF,垂足为B1,则BB1=AE=5(cm),所以B1F=8-5=3(cm).
因为平面ABFE∥平面DCGH,EF和HG是它们分别与截面的交线,所以EF∥HG.
过H作HC1⊥CG,垂足为C1,
则GC1=FB1=3(cm),
DH=12-3=9(cm).
(2)作ED1⊥DH,垂足为D1,B1P⊥CG,垂足为P,连接D1P,B1C1,则几何体被分割成一个长方体ABCD-EB1PD1,一个斜三棱柱EFB1-HGC1,一个直三棱柱EHD1-B1C1P.从而几何体的体积为
V=3×4×5+
| 1 |
| 2 |
| 1 |
| 2 |
(3)是菱形.
证明:由(1)知EF∥HG,同理EH∥FG.于是EFGH是平行四边形.
因为EF=
|
| 42+32 |
DD1=AE=5(cm),ED1=AD=3(cm),
HD1=4(cm),
所以EH=
|
| 32+42 |
所以EF=EH.
故EFGH是菱形.
点评:本题是中档题,考查组合体的体积,学生作图能力,空间想象能力,计算能力,线段的长度、体积的求解、以及证明的思路比较固定,难度不大.

练习册系列答案
相关题目
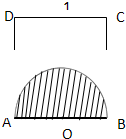
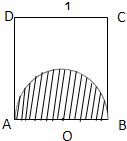 如图所示,以边长为1的正方形ABCD的一边AB为直径在其内部作一半圆.若在正方形中任取一点P,则点P恰好取自半圆部分的概率为( )
如图所示,以边长为1的正方形ABCD的一边AB为直径在其内部作一半圆.若在正方形中任取一点P,则点P恰好取自半圆部分的概率为( )
 如图所示,在矩形ABCD中,AB=4,AD=2,E是CD的中点,O 为AE的中点,F是AB 的中点.以AE为折痕将△ADE向上折起,使面DAE⊥面ABCE.
如图所示,在矩形ABCD中,AB=4,AD=2,E是CD的中点,O 为AE的中点,F是AB 的中点.以AE为折痕将△ADE向上折起,使面DAE⊥面ABCE.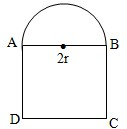 例1:某建材厂要生产一批如图所示的窗框,它由矩形ABCD与以AB为直径的半圆组成,已知窗框的框架的总面积为1平方米,制造矩形ABCD的直线型钢材每米价格为4元,制造半圆的弧形钢材每米价格为6元,设AB=2r,制造每扇窗框的材料价格为S元,把S表示成r的函数,并求S的最小值.
例1:某建材厂要生产一批如图所示的窗框,它由矩形ABCD与以AB为直径的半圆组成,已知窗框的框架的总面积为1平方米,制造矩形ABCD的直线型钢材每米价格为4元,制造半圆的弧形钢材每米价格为6元,设AB=2r,制造每扇窗框的材料价格为S元,把S表示成r的函数,并求S的最小值.