题目内容
 如图所示,四边形ABCD为矩形,AD⊥平面ABE,AE=EB=BC=2,F为CE上的点,且BF⊥平面ACE.
如图所示,四边形ABCD为矩形,AD⊥平面ABE,AE=EB=BC=2,F为CE上的点,且BF⊥平面ACE.(1)求证:AE⊥BE;
(2)设M在线段AB上,且满足AM=3MB,线段CE上是否存在一点N,使得MN∥平面DAE?若存在,求出CN的长;若不存在,说明理由.
分析:(1)由AD∥BC和AD⊥平面ABE证明AE⊥BC,再由BF⊥平面ACE得AE⊥BF,根据线面垂直的判定定理证出AE⊥平面BCE,即证出AE⊥BE;
(2)根据条件分别在△ABE中过M点作MG∥AE和△BEC中过G点作GN∥BC,根据线面平行的判定证出MG∥平面ADE和GN∥平面ADE,由面面平行的判定证出平面MGN∥平面ADE,则得到N点在线段CE上的位置.
(2)根据条件分别在△ABE中过M点作MG∥AE和△BEC中过G点作GN∥BC,根据线面平行的判定证出MG∥平面ADE和GN∥平面ADE,由面面平行的判定证出平面MGN∥平面ADE,则得到N点在线段CE上的位置.
解答:(1)证明:∵AD⊥平面ABE,AD∥BC
∴BC⊥平面ABE,∴AE⊥BC
又∵BF⊥平面ACE,∴AE⊥BF
∵BC∩BF=B,
∴AE⊥平面BCE,
∵BE?平面BCE,∴AE⊥BE;
(2)解:存在CN=
CE,使得MN∥平面DAE.
在△ABE中过M点作MG∥AE交BE于G点,在△BEC中过G点作GN∥BC交EC于N点,连MN,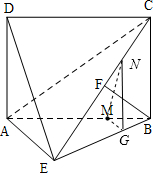
∵AM=3MB,∴CN=
CE
∵MG∥AE,MG?平面ADE,AE?平面ADE,∴MG∥平面ADE
同理可证,GN∥平面ADE,
∵MG∩GN=G,∴平面MGN∥平面ADE
又∵MN?平面MGN,∴MN∥平面ADE,
∵EB=BC=2,∴CE=2
∴CN=
∴BC⊥平面ABE,∴AE⊥BC
又∵BF⊥平面ACE,∴AE⊥BF
∵BC∩BF=B,
∴AE⊥平面BCE,
∵BE?平面BCE,∴AE⊥BE;
(2)解:存在CN=
| 1 |
| 4 |
在△ABE中过M点作MG∥AE交BE于G点,在△BEC中过G点作GN∥BC交EC于N点,连MN,

∵AM=3MB,∴CN=
| 1 |
| 4 |
∵MG∥AE,MG?平面ADE,AE?平面ADE,∴MG∥平面ADE
同理可证,GN∥平面ADE,
∵MG∩GN=G,∴平面MGN∥平面ADE
又∵MN?平面MGN,∴MN∥平面ADE,
∵EB=BC=2,∴CE=2
| 2 |
∴CN=
| ||
| 2 |
点评:本题是关于线线、线面和面面垂直与平行的综合题,利用垂直与平行的判定(性质)定理,实现线线、线面和面面的相互转化,属于中档题.

练习册系列答案
相关题目
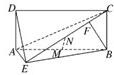 如图所示,四边形ABCD为矩形,BC⊥平面ABE,F为CE上的点,且BF⊥平面ACE.
如图所示,四边形ABCD为矩形,BC⊥平面ABE,F为CE上的点,且BF⊥平面ACE. 如图所示,四边形PCBM是直角梯形,∠PCB=90°,PM∥BC,PM=PC=AC=1,BC=2,∠ACB=120°,AB⊥PC.
如图所示,四边形PCBM是直角梯形,∠PCB=90°,PM∥BC,PM=PC=AC=1,BC=2,∠ACB=120°,AB⊥PC.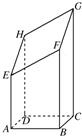 如图所示,以AB=4cm,BC=3cm的长方形ABCD为底面的长方体被平面斜着截断的几何体,EFGH是它的截面.当AE=5cm,BF=8cm,CG=12cm时,试回答下列问题:
如图所示,以AB=4cm,BC=3cm的长方形ABCD为底面的长方体被平面斜着截断的几何体,EFGH是它的截面.当AE=5cm,BF=8cm,CG=12cm时,试回答下列问题: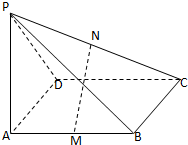 如图所示,四边形ABCD是矩形,PA⊥平面ABCD,△PAD是等腰三角形,M、N分别是AB,PC的中点,
如图所示,四边形ABCD是矩形,PA⊥平面ABCD,△PAD是等腰三角形,M、N分别是AB,PC的中点,