题目内容
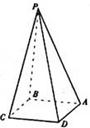 四棱锥P-ABCD的底面是边长为a的正方形,PB⊥平面ABCD.
四棱锥P-ABCD的底面是边长为a的正方形,PB⊥平面ABCD.(1)若面PAD与面ABCD所成的二面角为60°,求这个四棱锥的体积;
(2)证明无论四棱锥的高怎样变化.面与面所成的二面角恒大于90°.
分析:本题考查的知识点是棱柱、棱锥、棱台的体积及二面角的度量.(1)由PB⊥平面ABCD,我们易得∠PAB是面PAD与面ABCD所成二面角的平面角,∠PAB=60°代入易得到VP-ABCD=
•
a•a2=
a3(2)由于棱锥侧面PAD与PCD恒为全等三角形.作AE⊥DP,垂足为E,连接EC,则△ADE≌△CDE.∴AE=EC,∠CED=90°,故∠CFA是面PAD与面PCD所成的二面角的平面角.解三角形AEC可得
∠CFA的余弦值小于0,故面与面所成的二面角恒大于90°
| 1 |
| 3 |
| 3 |
| ||
| 3 |
∠CFA的余弦值小于0,故面与面所成的二面角恒大于90°
解答: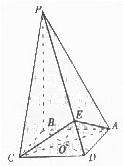 解(1)∵PB⊥平面ABCD,∴BA是PA在面ABCD上的射影,∴PA⊥DA
解(1)∵PB⊥平面ABCD,∴BA是PA在面ABCD上的射影,∴PA⊥DA
∴∠PAB是面PAD与面ABCD所成二面角的平面角,∠PAB=60°
而PB是四棱锥P-ABCD的高,PA=AB•tan60°=
a
∴VP-ABCD=
•
a•a2=
a3
证明:(2)不论棱锥的高怎样变化,棱锥侧面PAD与PCD恒为全等三角形.
作AE⊥DP,垂足为E,连接EC,则△ADE≌△CDE.
∴AE=EC,∠CED=90°,故∠CFA是面PAD与面PCD所成的二面角的平面角.
设AC与DB相交于点O,连接EO,则EO⊥AC.
a=OA<AE<AD=a
在△AEC中,cos∠AEC=
=
<0
所以,面PAD与面PCD所成的二面角恒大于90°
 解(1)∵PB⊥平面ABCD,∴BA是PA在面ABCD上的射影,∴PA⊥DA
解(1)∵PB⊥平面ABCD,∴BA是PA在面ABCD上的射影,∴PA⊥DA∴∠PAB是面PAD与面ABCD所成二面角的平面角,∠PAB=60°
而PB是四棱锥P-ABCD的高,PA=AB•tan60°=
| 3 |
∴VP-ABCD=
| 1 |
| 3 |
| 3 |
| ||
| 3 |
证明:(2)不论棱锥的高怎样变化,棱锥侧面PAD与PCD恒为全等三角形.
作AE⊥DP,垂足为E,连接EC,则△ADE≌△CDE.
∴AE=EC,∠CED=90°,故∠CFA是面PAD与面PCD所成的二面角的平面角.
设AC与DB相交于点O,连接EO,则EO⊥AC.
| ||
| 2 |
在△AEC中,cos∠AEC=
| AE2+EC2-(2•OA)2 |
| 2AE•EC |
(AE+
| ||||
| AE2 |
所以,面PAD与面PCD所成的二面角恒大于90°
点评:求这个四棱锥的体积,关键是要根据已知条件求出底面面积和棱锥的高,然后代入棱锥体积公式计算;证明无论四棱锥的高怎样变化.面与面所成的二面角恒大于90°,即证明二面角对应的平面角余弦值小于0.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
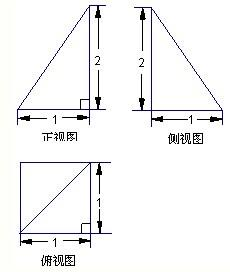 已知四棱锥P-ABCD的三视图如图所示,则这个四棱锥的体积为( )
已知四棱锥P-ABCD的三视图如图所示,则这个四棱锥的体积为( )A、
| ||
| B、1 | ||
C、
| ||
D、
|
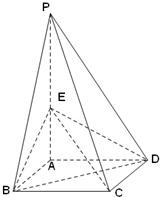 如图,四棱锥P-ABCD的底面是边长为1的正方形,侧棱PA⊥底面ABCD,且PA=2,E是PA的中点.
如图,四棱锥P-ABCD的底面是边长为1的正方形,侧棱PA⊥底面ABCD,且PA=2,E是PA的中点. 如图所示,四棱锥P-ABCD的底面是边长为a的正方形,侧棱PA⊥底面ABCD,侧面PBC内有BE⊥PC于E,且BE=
如图所示,四棱锥P-ABCD的底面是边长为a的正方形,侧棱PA⊥底面ABCD,侧面PBC内有BE⊥PC于E,且BE= 如图,ABCD是正方形,O是该正方形的中心,P是平面ABCD外一点,PO⊥底面ABCD,E是PC的中点.求证:
如图,ABCD是正方形,O是该正方形的中心,P是平面ABCD外一点,PO⊥底面ABCD,E是PC的中点.求证: