题目内容
已知A={a1,a2,a3,a4,a5},B={a12,a22,a32,a42,a52}, ai∈N(i=1,2,3,4,5)
设a1<a2<a3<a4<a5且A∩B={a1,a4},a1+a4=10,又A∪B元素之和为224,
求:(1)a1,a4 (2)A
设a1<a2<a3<a4<a5且A∩B={a1,a4},a1+a4=10,又A∪B元素之和为224,
求:(1)a1,a4 (2)A
(1)a1 =1,a4=9,(2)A={1,3,4,9,10}
(1)∵A∩B={a1,a4}且a1+a4=10,即两个完全平方数的和为10,
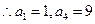 ……4分
……4分
(2)∵A∪B的元素之和为224,即a2+a3+a5+a12+a22+a32+a42+a52=224,
而a12+a42="82" ∴a2+a3+a5+a22+a32+a52="142 " ……8分
∵a4=9<a5若a5=11,则a2+a3+a22+a32=10这不可能
∴a5="10 " ……12分
∴a2+a3+a22+a32=32
若a32=a4=9得a2+a22="20 " ∴a2=4>a3 (矛盾)
从而a2=3,a3=4
∴A={1,3,4,9,10} ……14分
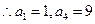 ……4分
……4分(2)∵A∪B的元素之和为224,即a2+a3+a5+a12+a22+a32+a42+a52=224,
而a12+a42="82" ∴a2+a3+a5+a22+a32+a52="142 " ……8分
∵a4=9<a5若a5=11,则a2+a3+a22+a32=10这不可能
∴a5="10 " ……12分
∴a2+a3+a22+a32=32
若a32=a4=9得a2+a22="20 " ∴a2=4>a3 (矛盾)
从而a2=3,a3=4
∴A={1,3,4,9,10} ……14分

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
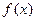
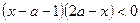
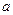
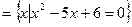 ,B=
,B=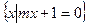 ,且
,且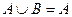 ,求实数
,求实数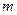 的值组成的集合。
的值组成的集合。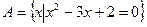 ,
,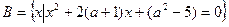
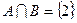 ,求实数
,求实数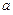 的值;
的值;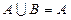 ,求实数
,求实数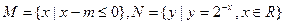 ,若
,若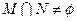 ,则实数m的取值范围是( )
,则实数m的取值范围是( )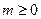
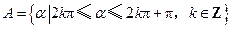 ,集合
,集合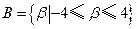 ,求
,求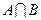 .
.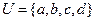 ,集合
,集合 ,
,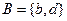 ,则(
,则(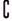 U
U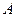 )∩
)∩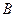 =( )
=( ) 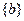


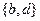
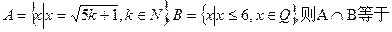 ( )
( ) B
B 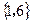 C
C 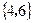 D
D 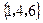
 的定义域为
的定义域为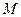 ,集合
,集合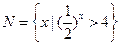 ,则
,则 ( )
( )